Кинематика колебательного движения

· Колебания– это движения или процессы, обладающие той или иной степенью повторяемости во времени.

Колебания широко распространены в природе и имеют место в самых разнообразных явлениях, например, качание маятника пружинных часов, мигание индикатора таймера, изменение значения переменного тока, величины напряжения на обкладках конденсатора, включенного в колебательный контур и т. п. Повторяющиеся процессы протекают внутри живых организмов, например, биение сердца, чередование промежутков сна и бодрствования, ритмы, сопровождающие работу человеческого мозга. Таким образом, колебания присутствуют как в живой, так и в неживой природе; в микроскопических и макроскопических процессах.

Важнейшая особенность колебательного движения состоит в том, что оно происходит в системах, занимающих ограниченную часть пространства. Так, совершая колебательное механическое движение, система движется около некоторого положения равновесия, но энергия системы не выходит за пределы границ системы. Колеблющаяся величина, заключена в некоторый интервал, содержащий ее среднее значение. Несмотря на качественное различие тех или иных колебательных процессов, все они могут быть описаны одними и теми же количественными законами.

· Свободные, или собственные колебания– это колебания, которые происходят в системе, выведенной из состояния равновесия и предоставленной самой себе.

· Гармоническимиколебанияминазывают колебания, при которых колеблющаяся величина изменяется во времени по закону синуса или косинуса. Гармонические колебания представляют собой простейшие колебания.

Уравнение гармоническименяющейся величины x может быть как с помощью функции синуса, так и с помощью функции косинуса следующим образом:

.

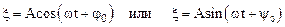В формулу (1.33) входят следующие величины:

· Амплитуда колебанийА – наибольшее значение колеблющейся величины x. Из (1.33) следует, что А>0.

· Фазаколебаний– 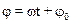– аргумент функции синуса или косинуса в уравнении гармонического колебания.

· Начальнаяфаза колебаний– 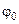значение фазы j в момент времени t=0.

При необходимости, переход от функции синуса к функции косинуса осуществляется по формулам приведения, при этом изменяется начальная фаза колебаний. Например, в формулах (1.33) .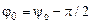

· ПериодколебанийТ – это время, за которое совершается одно полное колебание.

· Можно говорить, что период – это наименьший промежуток времени, по истечении которого колеблющаяся величина x имеет то же самое значение и ту же скорость изменения.

· Частота колебанийn (n, или f) – величина обратная периоду колебаний

.

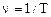· Круговая, илициклическая, частотаw связана с частотой n соотношением

.

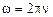Измеряется циклическая частота в с ^–1. Она показывает, какое число колебаний происходит за 2p секунд.

Используя определение периодичной функции – F(х)=F(х+Т), запишем:

.

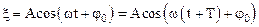Поскольку функция имеет период 2p, то сравнение фаз колебаний позволяет установить связь периода колебаний с циклической частотой:

,

отсюда следует, что

.

Частота показывает, какое число колебаний совершается за единицу времени (секунду). Измеряется частота в герцах: 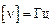. 1 Гц – это такая частота, при которой в единицу времени совершается одно колебание.

Скоростьизменения V и ускорение – a колеблющейся величины x определяется обычным образом (по формулам (1.4) и (1.7)):

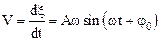
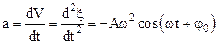
Начальную фазу колебаний, можно определить с помощью первого из уравнений (1.33) по известным начальным условиям x₀, V₀:

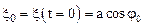и .

Откуда следует:

.

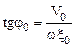Амплитуду гармонически колеблющейся величины можно вычислить по формуле: