Характеристик при движении по окружности
Обратимся вновь к рисунку 1.3, чтобы установить связь линейной и угловой скоростейпри движении по окружности. Для бесконечно малого угла поворота dφ путь dS, пройденный частицей равен длине дуги окружности, т. е.:
dS=Rdj.
На основании соотношения (1.9) модуль V линейной скорости найдем дифференцированием:
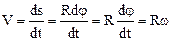
· Векторноепроизведениевекторов a и b есть вектор с(обозначается c=[a,b]), модуль которого равен произведению модулей векторов-сомножителей на синус угла между этими векторами. Направление вектора векторного произведения определяется по правилу буравчика (Б.II).
· Правилобуравчика (Б.II) для нахождения направления вектора векторного произведения c=[a,b]:
1. отложить векторы aи b от одной точки,
2. провести через них плоскость,
3. расположить буравчик перпендикулярно полученной плоскости,
4. вращать рукоятки буравчика от первого вектора-сомножителя aко второму b в направлении меньшего угла,
5. направление поступательного движения конца буравчика укажет направление вектора с векторного произведения.

|
Рис. 1.4.
К определению векторного произведения векторов.
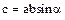 , или , или 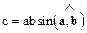 , где , где 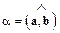 .
Модуль векторного произведения векторов равен площади параллелограмма, построенного на векторах сомножителях a и b, как на сторонах .
Модуль векторного произведения векторов равен площади параллелограмма, построенного на векторах сомножителях a и b, как на сторонах
|
Анализируя направления векторов V, R и w (см. рис. 1.3) приходим к выводу, что они связаны посредством следующего векторного произведения:
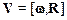 .
.
Формулу (1.21) называют формулойЭйлера.
Покажем, что движение материальной точки по окружности с постоянной по модулю линейной скоростью представляет собой равнопеременное движение. Поскольку мгновенная линейная скорость V всегда направлена по касательной к траектории в данной ее точке, то (см. рис. 1.5), оставаясь постоянной по модулю, она непрерывно изменяется по направлению, поэтому скорости движущейся точки в положениях А и В не равны: VA ¹ VB. Изменение вектора скорости свидетельствует о том, что материальная точка на окружности испытывает ускорение.
|
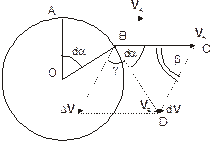
| Рис. 1.5. К анализу равномерного вращательного движения точки. AB=ОА=R, R – радиус окружности |
Пусть в момент времени t материальная точка находилась в точке А траектории, а через малый промежуток времени dt переместилась в близко расположенную точку В (на рисунке 1.5 дуга АВ для наглядности показана увеличенной). Изменение скорости за время dt равно разности dV=VB – VA, показанной на рисунке.
Рассмотрим треугольники АОВ и CВD. Эти треугольники подобны: они равнобедренные (OA=OB=R и ВС=BD=V) и имеют равные углы ÐAOB=ÐDBC=da (это углы со взаимно перпендикулярными сторонами). Из подобия треугольников АОВ и CВD следует, что
AB:AO=DC:BD. (*)
Длина дуги AB=Rda (da – центральный угол, опирающийся на дугу АВ), из треугольника ОАВ выразим хорду АВ: AB=2Rsin(da/2)»Rda. Для бесконечно малого промежутка времени dt угол da мал, поэтому длина дуги приблизительно равна хорде:
CD=dV=2Vsin(da/2)»Vda=adt.
Подставляя полученные величины отрезков в пропорцию (*), имеем
Rda:R=adt:V.
Откуда следует: что величина ускорения численно равна:
a=dV/dt=Vda/dt=Vw. (**)
Используя соотношение (1.20) получим, что
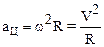 .
.
Для определения направления вектора ускорения рассмотрим треугольник ВСD. Направление вектора а, как уже отмечено, совпадает с направлением вектора dV, в нашем случае – с направлением отрезка CD. Из треугольника ВCD следует, что угол b – угол между векторами VА и dV равен (p-da)/2. Очевидно, что при da®0 угол b®p/2. Таким образом, вектор dV, а значит и вектор ускорения а, при dt®0 стремятся к положению нормали к вектору скорости V.
Таким образом, при движении по окружности с постоянной по величине линейной (или угловой) скоростью, материальная точка испытывает постоянное ускорение, направленное по радиусу к ее центру. Такое ускорениеназывают центростремительным. Формулу для центростремительного ускорения в векторном виде записывают, используя векторное произведение векторов линейной V и угловой w скорости:
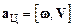 .
.
Используя соотношение (1.21) и векторное тождество
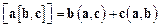
последнюю формулу можно записать так:
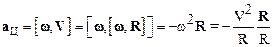 .
.
Вектор R/R=n – есть вектор внешней нормали к траектории.
Дата добавления: 2015-08-08; просмотров: 793;
