Скорость и ускорение. · Механика– раздел физики, изучающий закономерности механического движения тел и причины, вызывающие (или изменяющие) его.

Лекционный блок

Глава 1. Кинематика

Основные понятия

· Механика– раздел физики, изучающий закономерности механического движения тел и причины, вызывающие (или изменяющие) его.

· Механическоедвижение– процесс изменения с течением времени взаимного расположения тел или частей тела относительно друг друга.

· Кинематика– раздел физики, изучающий механическое движение тел, безотносительно к причинам, вызывающим это движение.

· Классическая (нерелятивистская ) механика или механикаНьютона – нерелятивистская теория движения макроскопических объектов.

· Нерелятивистскаятеория –теория движения тел со скоростями V, гораздо меньшими скорости света с: V<<с.

· Основнаязадачакинематики (механики) состоит в определении положения и скорости движущейся материальной точки (тела) в произвольный момент времени.

· Материальнаяточка– модель реального тела:

1) размеры которого стремятся к нулю, говорят: материальная точка не имеет размеров,

2) имеет не равную нулю массу.

В конкретной задаче материальной точкой можно считать тело, размеры которого много меньше, чем расстояния между телами, или размеров области, в которой происходит движение.

· Абсолютнотвердоетело– тело, расстояние между любыми точками которого всегда остается неизменным. Такое тело не способно деформироваться, но под действием внешних сил в нем могут возникать внутренние напряжения, силы упругости и давления.

· Поступательнымдвижениемназывают движение, при котором любая прямая, проведенная в теле остается параллельной сама себе.

Для указания положения материальной точки в пространстве и описания изменения этого положения во времени вводят систему отсчета.

· Системаотсчета – совокупность: 1) тела отсчета (тела, по отношению к которому определяется положение некоторой материальной точки); 2) системы координат с началом отсчета в точке, выбранной на теле отсчета, 3) часов – прибора для отсчета времени. Можно говорить, что система отсчета представляет собой систему координат, жестко связанную с телом отсчета и часы.

· Радиус-векторr материальной точки – это вектор, проведенный из начала координат системы отсчета к этой материальной точке.

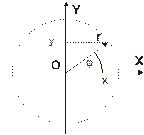
Наиболее часто при решении задач на плоскости вводят декартовы прямоугольные координаты (x, y) и полярные координаты (r, φ); в трехмерном пространстве – декартовы прямоугольные (x, y, z), цилиндрические (z, r, φ) и сферические (r, Θ, φ) системы координат. В декартовой системе координат координаты (x, y, z) материальной точки М определяют как проекции радиус-вектора r этой точки на соответствующие оси системы координат. Взаимосвязь названных систем координат иллюстрируют приведенные ниже рисунки.

Рис.1.1а. Декартовы x,y и и полярные r, j, координаты

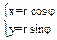
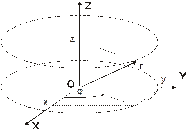
Рис.1.1b. Соответствие декартовых x,y,z и и цилиндрических r, j, z координат

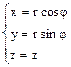
Рис.1.1с. Соответствие декартовых x,y,z и сферических r, q, f координат

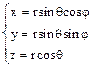
Движение материальной точки в пространстве сопровождается изменением ее координат (и ее радиус-вектора) с течением времени. Процесс движения может быть описан системой уравнений, представляющей собой параметрическое уравнениетраектории:

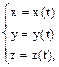
или уравнением для радиус-вектора:

,

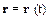где радиус вектор r=(x,y,z).

· Траекторияматериальной точки может быть определена следующими способами:

1) линия, вдоль которой движется материальная точка (центр масс материального тела) в данной системе отсчета,

2) геометрическое место концов радиус-векторов материальной точки.

Уравнение траектории в явном виде, как уравнение, связывающее между собой пространственные координаты движущейся материальной точки, может быть получено исключением времени из системы уравнений (1.1).

· Путь(длинапути) – скалярная величина численно равная длине участка траектории, пройденного материальной точкой от начального положения С до конечного В (см. рис. 1.2).

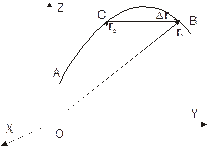
Рис. 1.2. АСВ - траектория движения материальной точки, r0 и r – ее начальный и конечный радиус-векторы, Dr=S – вектор перемещения

· Перемещение– вектор S направленный из начального положения движущейся материальной точки в ее конечное положение.

Вектор перемещения S можно определить как приращение Dr радиус-вектора материальной точки: S=Dr = r₁ – r₀. Рисунок 1.2 позволяет сделать вывод, что модуль вектора перемещения совпадает с длиной пройденного пути лишь при прямолинейном движении.

Скорость и ускорение

Изменение положения материальной точки в пространстве с течением времени характеризуют с помощью скорости. В физике используется понятие "скорость" используется в нескольких различных смыслах.

· Средняяскоростьдвижения – векторная величина, равная отношению вектора перемещения материальной точки S=Dr ко времени Dt, за которое это перемещение произошло:

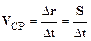
Формальное, количественное определение каждой новой физической величины требует установления ее физического смысла, позволяющего с той или иной степенью наглядности представить конкретную ситуацию. Физический смысл величин устанавливается по определенной схеме. Так, если в формуле (1.3) для средней скорости положить Dt=1 с, то она принимает вид: 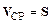. Поэтому, средняя скорость показывает, какое перемещение совершает материальная точка за единицу времени. Последнее равенство указывает также, что вектор средней скорости V_CP направлен вдоль вектора перемещения S.

Соотношение (1.3) позволяет установить размерность единицы измерения скорости. Для этого в определение величины подставляют (не обращая внимания на векторный характер записи) размерность всех входящих величин:

.

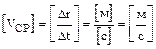· Единицаскорости – 1 м/с – есть скорость такого движения, при котором материальная точка за одну секунду проходит расстояние в 1 метр.

· Мгновеннаяскорость– скорость материальной точки в данный момент времени, в данной точке траектории.

Количественное определение мгновенной скорости V требует дополнительных рассуждений. Средняя скорость, характеризует движение в целом, и не является его детальной характеристикой. Мгновенную скорость можно определить путем предельного перехода в соотношении (1.3) при Dt®0:

.

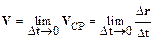Из курса математического анализа известно, что такой предел представляет собой первую производную радиус-вектора r по времени t:

.

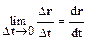Таким образом:

· Мгновеннаяскорость – векторная физическая величина, равная первой производной радиус-вектора r материальной точки по времени:

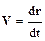
Из приведенных определений следует, что в общем случае вектор средней скорости V_CP направлен вдоль перемещения S=Dr, т. е. вдоль секущей – линии, проходящей через начальное и конечное положения движущейся точки. Из курса математического анализа известно, что в пределе, при Dt®0, когда Dr®0, секущая некоторой кривой совпадает с касательной к ней, поэтому мгновенная скорость V направлена по касательной к траектории.

Мгновенная скорость V, как и средняя, показывает, какое перемещение совершила бы движущаяся материальная точка за единицу времени, обладая постоянной скоростью V.

· Средняяпутеваяскорость– скалярная величина, равная отношению всего пути, пройденного материальной точкой, ко всему времени движения, т. е. к промежутку времени, за который этот путь был пройден:

.

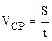Очевидно, мгновенная скорость движения материальной точки может меняться во времени. Характеристикой такого изменения служит ускорение.

· Среднееускорениеравно отношению изменения скорости DV к промежутку времени Dt, за которое это изменение произошло:

.

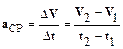Положив в этом определении Dt=1с, легко понять, что среднее ускорение показывает, на сколько изменилась скорость за единицу времени. Измеряется ускорение в следующих единицах:

.

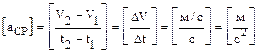Ускорение, подобно скорости, может изменяться с течением времени.

· Мгновенноеускорение– это ускорение материальной точки в данный момент времени, в данной точке траектории.

Проводя рассуждения, как при определении мгновенной скорости, можно сделать вывод, что:

· Ускорение – векторная физическая величина равная первой производной скорости материальной точки по времени или, соответственно, второй производной ее радиус-вектора по времени:

.

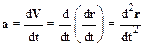Положив в соотношении (1.7) промежуток времени dt=1c, получим 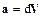, что позволяет понять физический смысл ускорения. Ускорение показывает, на сколько изменяется скорость за единицу времени.