Нормальное, тангенциальное и полное ускорения

Взаимосвязь угловых и линейных характеристик можно рассмотреть на основе общих соображений. Пусть V мгновенная линейная скорость материальной точки, движущейся по окружности, w – ее угловая скорость. Введем единичный вектор касательной t, связанный с движущейся материальной точкой. Тогда скорость V можно записать так:

,

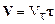здесь V_t=V – проекция вектора скорости на направление вектора касательной. Дифференцируя (1.25) по времени, получим:

.

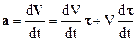Преобразуем второй член последнего соотношения:

.

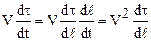Как видно из рисунка (1.5)

.

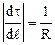Направление dt/dℓ совпадает с направлением вектора внутренней нормали n. Окончательно (1.26) запишем следующим образом:

.

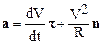В соотношении (1.29) первое слагаемое представляет собой тангенциальной ускорениеа_t, второе – нормальное а_Н или центростремительное ускорение. Таким образом,

:

полное ускорениедвижущейся точки равно векторной сумме нормального и тангенциального ускорений. Модуль полного ускорения определяется соотношением:

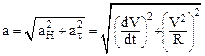
Воспользуемся формулой Эйлера (1.21): 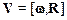. Дифференцируя по времени (1.31), имеем:

,

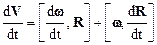где dw/dt=e угловое ускорение, dR/dt=V – мгновенная линейная скорость материальной точки.

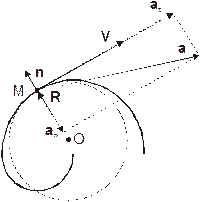
Рис. 1.6.   V – мгновенная линейная скорость, at – тангенциальное, an – нормальное и a – полное ускорение частицы. О – центр касательной окружности радиусом R, n – внешняя нормаль к траектории движения

Из рисунка 1.6 видно, что множитель 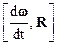представляет собой тангенциальное ускорение, а 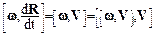– нормальное или центростремительное ускорение.

Таким образом (1.32) можно привести к виду: . (1.32а)