Сложение колебанийодного направления

Пусть материальная точка одновременно участвует в двух колебаниях x₁ и x₂ одного направления и одной частоты w:

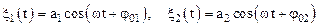
По принципу суперпозиции результирующее смещение равно алгебраической сумме смещений, полученных в каждом из колебаний, т. е.:

.

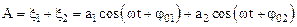Предположим, что амплитуды обоих колебаний равны, т. е. а₁=а₂=а. Используем тригонометрическую формулу для суммы двух косинусов и преобразуем формулу (1.39):

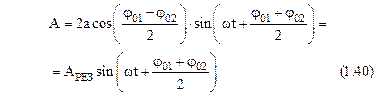
Таким образом, при суперпозиции колебаний одной частоты, одного направления и одинаковой амплитуды возникает гармоническое колебание с той же самой частотой w, и амплитудой, зависящей от разности начальных фаз колебаний и равной

.

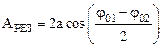В частности: при j₁₀=j₂₀ имеем А_РЕЗ=2а, при j₁₀=j₂₀±p амплитуда результирующего колебания равна нулю.

Биения

Рассмотрим суперпозицию двух гармонических колебаний одинаковой амплитуды и одного направления, частоты которых w₁ и w₂ отличаются незначительно (w₁»w₂=w)

, .

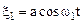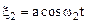Результирующее колебание равно:

.

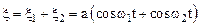Используя известные тригонометрические формулы, приведем (1.41) к следующему виду

.

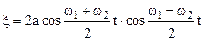Очевидно, что первый сомножитель гармонически изменяется с частотой w=(w₁+w₂)/2»w₁»w₂. Второй множитель осциллирует с малой частотой (w₁-w₂)/2, а значит, имеет большой период. Таким образом, колебание (1.43) можно рассматривать как гармоническое колебание с частотой w:

,

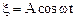амплитуда которого А равна:

.

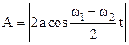Амплитуда медленно изменяется во времени – пульсирует.

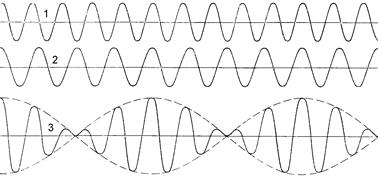
Характер изменения во времени величины x, порожденной наложением колебаний с отношением частот 8:10 показан на рисунке 1.7.

Изображенное на рисунке постепенное нарастание и уменьшение амплитуды результирующих колебаний и носит название “биения”.

Используя условие периодичности функции x(t)=x(t+T) можно показать, что при рациональном отношении частот колебаний w₁:w₂=n₁:n₂, (n₁:n₂ – целые числа) функция x является периодической с периодом Т равным

.

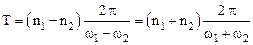Рис. 1.7.

(1) - колебания x1 = а cos 10wt, (2) колебание x2 = а cos 8wt, (3) результирующее колебание

Если частоты исходных колебаний не соизмеримы, т. е. их отношение w₁:w₂ не равно отношению некоторых целых чисел n₁ и n₂, то результирующее колебание не является периодическим.