Сложение взаимно перпендикулярных колебаний. Сложение колебаний c рациональным отношением частот, но направленных вдоль взаимно перпендикулярных осей X и Y

Сложение колебаний c рациональным отношением частот, но направленных вдоль взаимно перпендикулярных осей X и Y

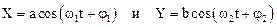
экспериментально исследовал А. Лиссажу. Он показал, что точка, участвующая в таких колебаниях, движется по плоским замкнутым траекториям, которые получили, в последствии, название фигурЛиссажу.

Пусть материальная точка участвует в двух колебаниях, определяемых уравнениями (1.46). Найдем уравнение траектории Ф(X,Y)=0 материальной точки на координатной плоскости X,Y. Для упрощения предположим, что частоты колебаний равны, а начальная фаза первого колебания равна нулю (этого можно добиться соответствующим выбором начального момента времени), начальную фазу второго колебания обозначим через j. Уравнения колебаний примут вид:

.

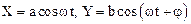Для нахождения траектории (исключения параметра t) поступим следующим образом: из первого уравнения системы (1.47) выразим coswt,

,

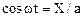тогда:

.

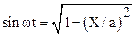Представляя cos(wt+j) как косинус суммы двух углов из второго уравнения (1.47) имеем

.

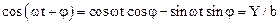Используя выражения для тригонометрических функций аргумента wt, соотношение (1.48) можно записать следующим образом:

.

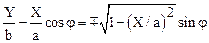Возводя в квадрат и произведя перегруппировку, получим:

.

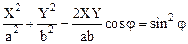Из аналитической геометрии известно, что уравнение (1.49) является уравнением эллипса, оси которого повернуты относительно осей координат X и Y. Ориентация осей эллипса и размеры его полуосей достаточно сложно зависят от разности фаз колебаний j=j₂-j₁=j₂.

Частные случаи.

1. Разность фаз исходных колебаний равна нулю (j=0). Уравнение (1.49) принимает вид:

,

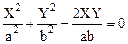т. е. представляет собой полный квадрат, поэтому:

.

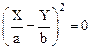Решением полученного уравнения является функция

.

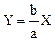2. Разность фаз колебаний равна ±p. Уравнение (1.49) приводится к виду

.

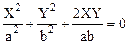Аналогично предыдущему случаю получаем:

.

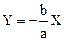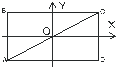
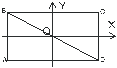
Уравнения (1.50) и (1.51) являются уравнениями прямых, тангенсы наклона которых равны b/a и -b/a, соответственно. Частица движется по соответствующей диагонали прямоугольника ABCD со сторонами a и b (см. рис. 1.8).

а

b

Рис. 1.8. a - движение описывается уравнением (1.50), и b - уравнением (1.51)

3. Разность фаз колебаний равна p/2. Уравнение результирующего движения (1.49) принимает вид

,

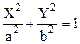т. е. представляет собой эллипс, приведенный к координатным осям X и Y, полуоси эллипса равны амплитудам a и b складывающихся колебаний.

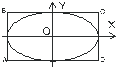
Рис. 1.9. Результат наложения взаимноперпендикулярных колебаний с разностью фаз равной p/2

4. При произвольной разности фаз j колебаний траектория представляет собой эллипс, вписанный в прямоугольник со сторонами 2a и 2b. Траектории, рассмотренные в пунктах 1 и 2 можно рассматривать как эллипсы, вырожденные в отрезок. Если полуоси эллипса (амплитуды складываемых колебаний) равны между собой, то эллипс вырождается в окружность (a=b).

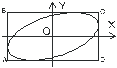
Рис. 1.10. Результат наложения взаимно перпендикулярных колебаний с произвольной разностью фаз

5. Разность фаз j определяет также направление движения материальной точки по траектории. Уравнения (1.47) в параметрической форме при величине j равной -p/2 могут быть записаны так:

.

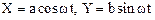После начала движения, т. е. при t>0 величина Х начнет уменьшаться, Y – будучи величиной положительной, будет возрастать. Этим изменениям, как видно из рисунка 1.11а, соответствует движение материальной точки со скоростью V против направления движения часовой стрелки. Если разность фаз j равна p/2, то уравнения (1.47) имеют вид

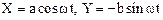
с началом движения координаты X и Y будут уменьшаться, что указывает на то, что точка движется по эллипсу в направлении движения часовой стрелки (см. рис. 1.11b).

6. Если частоты взаимно перпендикулярных колебаний не равны друг другу (w_X¹w_Y), то траектории движущихся точек представляются сложными кривыми. Во всех случаях, когда отношение w_X/w_Y является рациональным числом, траектория точки является замкнутой линией. Вид траектории зависит также от разности фаз исходных колебаний.

a

b

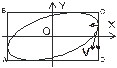
Рис 1.11. К вопросу о направлении движения частицы. Vуказывает направление скоростей частиц, стрелки – составляющие скоростей вдоль осей координат

Если отношение частот колебаний вдоль осей Х и Y (w_X:w_Y) не является рациональным числом, то траектория точки, участвующей в этих колебаниях – незамкнутая линия. С течением времени линия заполняет равномерно всю прямоугольную часть координатной плоскости размером 2a ´ 2b.