Общие характеристики волны
· Волновоеполе – область пространства, в которой существуют колебания.
· Волноваяповерхность – геометрическое место точек постоянной фазы.
· Волновойфронт – волновая поверхность, до которой в данный момент времени распространились колебания. Можно говорить также, что:
· Волновойфронт – поверхность, отделяющая волновое поле от области, в которой еще не началось колебательное движение. Иначе, волновой фронт – геометрическое место точек, до которых к данному моменту времени дошли колебания, таким образом, он является передним краем волны, граничащим с невозмущенной средой.
Форма волновой поверхности зависит от симметрии излучателя: так колебания от точечного источника, распространяющиеся в изотропной и однородной среде, имеют сферический волновой фронт, в иных случаях фронт может иметь вид плоскости, цилиндра и т. п. Соответственные волны называются сферическими, плоскими или цилиндрическими.
· Волновойлуч – линия, определяющая направление распространения колебаний и переноса энергии. В однородной и изотропной среде волновые лучи ортогональны по отношению к волновому фронту. Если волновой фронт плоский, то лучи параллельны между собой.
Как уже отмечено, в волновом поле определена периодическая функция от аргументов t, и X. Найдем период Т волны во времени, для чего используем условие периодичности функции косинуса, и запишем:
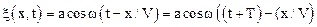 ,
,
что равносильно условию:
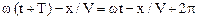 ,
,
откуда следует 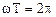 ,
,
или:
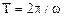 .
.
Последняя формула показывает, что период волны определяется периодом колебаний источника (ср. (1.52)).
· Периодволны – время, за которое совершается полное колебание в источнике волны.
· Частотаволны – величина обратная периоду колебаний
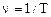 .
.
Исследуем пространственную периодичность волны. Обозначим пространственный период через l. Используя условие периодичности функции косинуса, можно записать:
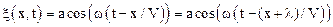 .
.
Это равенство выполняется, если
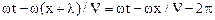 ,
,
откуда следует, что
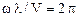 ,
,
или
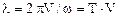 .
.
Величину l, являющуюся периодом волны в пространстве называют длиной волны.
· Длинаволны – расстояние, на которое распространяется волна за один период колебаний.
Используя определение частоты колебаний n, запишем
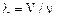
Длину волны определяют также как минимальное расстояние между двумя точками пространства, в которых колеблющаяся величина имеет одно и то же значение, поэтому можно дать другое определение:
· Длинаволны есть наименьшее расстояние между точками пространства, в которой колебания происходят в одной фазе.
Уравнение волны позволяет:
· определить значение колеблющейся величины в произвольной точке пространства в произвольный момент времени,
· изучать характер изменения колеблющейся величины в некоторой точке пространства (при фиксированной координате),
· для некоторого фиксированного момента времени позволяет исследовать распределение значений колеблющейся величины в пространстве.
Используя определение периода и длины волны уравнениебегущей волны, взятое, например, в виде (1.56) можно записать следующим образом:
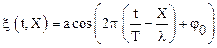 .
.
Дата добавления: 2015-08-08; просмотров: 770;
