Cedil;Приведенная характеристика насоса

Из формулы (5) следует, что напор в точке выхода жидкости из насоса равен напору, развивае­мому насосом и уменьшенному на величину потерь во всасывающем трубопроводе.

Графическая характеристика на­соса Н-Q (рис. 7), построен­ная с учетом потерь во всасываю­щем трубопроводе, называется при­веденной характеристикой.

Для построения графической характерис­тики всасывающего трубопровода воспользуемся уравнением (5). При заданном расчетном расходе Q_p определим h_вс, которые можно выразить как функцию подачи:

h _{w вс} = S_всQ² (6)

Задаваясь подачей Q_x, получим характеристику всасывающего трубопровода h _{w вс}

Подобные расчеты можно произ­вести и для напорных коммуни­каций насосной станции. Введя поправку h_{w н} в приведенную ха­рактеристику Н- Q' на потери в напорных коммуникациях, получим характеристику Н- Q", приведенную к точке выхода напорных водо­водов с насосной станции.

Аналогично можно построить графическую характеристику системы «водоводы – сеть».

Лекция № 6

Тема: Законы подобия насосов. Коэффициент быстроходности

Подобие насосов. Сложный характер движения перекачиваемой жидкости в рабочих органах ло­пастных насосов приводит к тому, что задача создания современных высокопроизводительных машин, от­вечающих сложному комплексу тре­бований , решается, наряду с расчетно-теоретической разработкой конструкций их про­точной части, путем проведения испытаний в лабораторных и натур­ных условиях. При проектирова­нии новых насосов используются также опытные данные, получаемые в процессе эксплуатации анало­гичных насосов на действующих станциях.

Предварительное определение расчетных параметров проектируе­мой машины, исследования рабочих режимов на моделях и распро­странение полученных результатов на натурные насосы возможно на основе теории о механическом по­добии движения реальной жид­кости. Главное положение этой теории заключается в необходи­мости выполнения условий геометри­ческого, кинематического и дина­мического подобия.

Геометрическое подобие в гид­ромеханике означает подобие всех поверхностей, ограничивающих и направляющих поток. При моде­лировании гидравлических машин два насоса могут быть названы подобными, если все линейные раз­меры одного из них (модель) в одинаковое число раз меньше или больше соответствующих размеров другого (натура). Математически геометрическое подобие сравниваемых насосов определяется посто­янством линейного коэффициента подобия:

Mi = D_H/D_M = bн/bм =... = const, (1)

где = D_H, D_M, bн, bм — соответственно диаметр и высота рабочих колес модельного и натур­ного насосов.

Геометрическое подобие означает также постоянство отношений лю­бых других размеров у модели и натуры.

Очевидно, что в осевых насосах геометрическое подобие подразуме­вает равенство углов установки лопастей рабочего колеса: j_м = j_н.

Строго говоря, геометрическое по­добие означает также подобие шеро­ховатостей обтекаемых потоком по­верхностей и зазоров между дви­жущимися и неподвижными деталя­ми насосов. Следовательно, для пол­ного его соблюдения необходимо, чтобы относительные шероховатости D/D и относительные зазоры d/ D , где D и d — соответственно экви­валентная абсолютная шерохова­тость и зазор, были одинаковыми. Но выполнение этого требования в практике моделирования гидравли­ческих машин возможно далеко не всегда. Действительно, при значе­ниях М_l = 20÷30 какие-либо высту­пы или неровности размером 1—2 мм точно воспроизвести на модели не удается.

Кинематическое подобие в общем виде означает, что безразмерные по­ля скоростей в рассматриваемых потоках должны быть одинаковы, т. е. отношения скоростей всех соответствующих частиц жидкости, участвующих в движении, должны быть равны между собой, а траек­тории движения в сравниваемых гид­равлических системах — геометри­чески подобны. Применительно к насосам это, в частности, означает подобие параллелограммов скоро­стей в соответствующих точках пото­ка во всех элементах проточной части двух геометрически подобных машин, ра0отающих в одинаковых режимах. Математически условия кинематического подобия могут быть выражены в виде ряда отношений:

J_н/J_м = w_н /w_м = u_н /u_м =n_нD_н / n_мD_м = ...сonst

Для соблюдения требований ки­нематического подобия необходима также выдерживать постоянным от­ношение скорости протекания жид­кости к скорости движения вращаю­щихся деталей, т. е.

J_м/ u_м = J_н/ u_н = сonst

Используя геометрическое подо­бие, из которого следует, что J µ Q/D² и u / µ nD ^, получаем еще одно условие кинематического подо­бия, представляющее чрезвычайно большой практический интерес при моделировании насосов:

Q_м / n _м D_м = Q_н / n _н D_н = сonst (2)

Динамическое подобие кроме соб­людения условий геометрического и кинематического подобия означает пропорциональность сил, действую­щих в соответствующих точках пото­ка. При отнесении к этим силам дав­ления, вязкости, сил тяжести и инер­ции динамическое подобие в общем виде обусловливается, как это хоро­шо известно, равенством чисел Эйле­ра, Рейнольдса, Фруда и Струхаля:

Eu= P/(rJ²); Re =Jl/n, Fr= J² /gl, St= Jt/l (3)

где l— характерный линейный размер; n — кинематическая вязкость жидкости; t— вре­мя.

Все эти критерии являются опре­деляющими лишь тогда, когда они выражены через исходные величины, задаваемые в начальных и граничных условиях. В противном случае каж­дый из определяющих критериев перейдет в неопределяющие или зависимые критерии. В частных за­дачах гидромеханики число опре­деляющих критериев, как правило, меньше указанных четырех.

В практике моделирования гид­равлических машин очень большое значение имеет критерий подобия Эйлера. Применительно к рассматри­ваемым условиям он может быть вы­ражен следующим образом:

Еu= P/(rJ²=gH /(J²). (4)

Заменяя скорость пропорцио­нальным отношением подачи к квад­рату диаметра рабочего колеса, по­лучим:

Еu= gHD⁴ /(Q²).

Следовательно, условие подобия может быть записано в виде:

Q_н / D_н ² 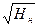= Q _м / D_м ² 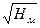5)

Уравнение (5) устанавливает зависимость между двумя основными энергетическими параметрами (по­дачей и напором) модельного и на­турного насосов.

Соблюдение условия равенства чисел Рейнольдса в натуре и на модели при решении практических задач осуществимо далеко не всегда. Теоретический анализ возможности выполнения этого условия показы­вает, что кинематическая вязкость жидкости модельного потока n_м должна быть меньше кинематической вязкости натурного потока n _н в М 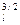раз. При испытании модели осевого насоса, имеющего в натуре рабочее колесо диаметром D_н = 4 м, на экспериментальной установке с колесом диаметром D_м = 0,2 м коэф­фициент подобия будет равен 20. Тогда кинематическая вязкость жид­кости модельного потока для соблю­дения равенства Re_м = Re_н должна быть меньше кинематической вяз­кости воды в 89,5 раза, а капельных жидкостей столь малой вязкости в природе не существует.

Формулы пересчета. Принимаем, что геометрически подобные друг другу рабочие колеса однотипных на­сосов диаметрами D_м и D_н вра­щаются с частотами n _н и n_м , соответственно создавая при этом напоры Н_м и Н _н и обеспечивая подачи Q_м и Q _н.

Из основного., уравнения для условий безударного входа имеем, что при n _м и D _м напор насоса

H_м = k _м h _г u_2н J_2н • cos a_2м / g

и соответственно при n_н и D _н

H_н= k н h _г u_2м J_2м • cos a_2н / g

Отношение этих напоров

=

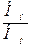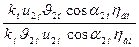
Исходя из условий геометрическо­го подобия, можно считать, что k_н = k_м, а подобие параллелограммов скоростей, вытекающее из условий кинематического подобия, означает равенство углов: a_2н = a_2м. Отноше­ние скоростей u₂. и J₂, согласно математическому выражению усло­вий кинематического подобия пропорционально от­ношению произведений nD. Следовательно, если подобные друг другу рабочие колеса насосов будут вращаться с различной часто­той, то для создаваемых ими напо­ров можно написать соотношение

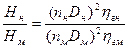(6)

Как уже известно, подача насоса из­меняется пропорционально измене­нию площади выходного сечения рабочего колеса и радиальной со­ставляющей абсолютной скорости на выходе, тогда

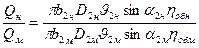
Поскольку рабочие колеса рассматриваемых насосов геометри­чески подобны, т. е. b_2н/b_2м = D _2н / D _{2м ,} то в общем случае с учетом условий кинематического подобия

a_2н=a_2м и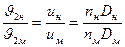

можно написать:

(7)

Мощность насоса изменяется пропорционально произведению QHh . Подставляя вместо Q и Н со­ответствующие величины из урав­нений (6) и (7), имеем:

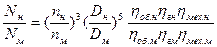(8)

Уравнения (6) — (8), полу­ченные на основе подобия лопастных насосов, называют формулами пере­счета. Эти формулы дают возмож­ность с большой точностью рассчи­тать основные параметры проекти­руемого насоса, если известны пара­метры насоса, геометрически ему подобного. Наконец, формулы пере­счета испытания насоса при одной частоты вращения определить его параметру для другой частоты.

Для пересчета КПД насоса с модели на натуру был предложен эяд формул, но широкого распрост­ранения они не получили. Причина этого заключается в том, что лопастных насосов значение КПД в большой мере определяется объ­емными и механическими потерями.] Поэтому пересчет КПД с модели на натуру без разделения его на составляющие не оправдывает себя.

Как отмечалось ранее , самым трудным является определе­ние гидравлического КПД. Совре­менные методы его вычисления сво­дятся к использованию зависимости h_г от размеров насоса и отно­сительной шероховатости поверх­ностей проточной части при условии работы модели в области автомодельности. Наиболее оправдала себя полуэмпирическая формула А. А. Ло­макина:

h_гн = 1 - (1-h_гм) ( 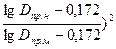(9)

где D_пр=(4¸4,5)10³ 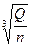- приведенный диаметр входа в рабочее колесо насоса, мм.

Объемные потери и механические потери в подшипниках и сальниках как немоделируемые должны под-считываться по соответствующим формулам (см. § 7).

При малом отличии n_н от n_м и D_н от D_м, а также при предва­рительных расчетах можно принять в первом приближении равными все значения h_ни h_м. Благодаря этому формулы пересчета можно представить в более удобном для решения практических задач виде:

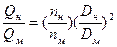
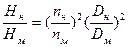(10)

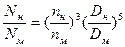
В том случае, когда один и тот же насос, перекачивающий одну и ту же жидкость, испытывается при различных частотах вращения n₁ от n₂ формулы пересчета еще более упрощаются:

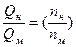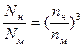; ; (11)