Эффект Доплера. В соответствии с принципом Доплера, волна, испущенная источником, распространяется в пространстве независимо от своего источника

В соответствии с принципом Доплера, волна, испущенная источником, распространяется в пространстве независимо от своего источника. Скорость ее распространения определяется характером волны и свойствами среды, и не зависит от скорости движения источника. Однако, частота (и длина волны) зависит как от скорости источника, так и от скорости наблюдателя (приемника), регистрирующих волну.

· Изменение частоты волны, воспринимаемой наблюдателем в зависимости от относительного движения источника волн и самого наблюдателя, носит название эффектаДоплера. Если источник волны и/или наблюдатель, ее воспринимающий, движутся относительно среды, в которой распространяется волна, то частота, измеряемая наблюдателем, будет зависеть не только от частоты посылаемой волны, но также от направления и скоростей движения, как источника, так и наблюдателя.

А	В
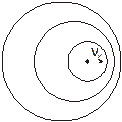
Рис. 1.20. Волновые поверхности неподвижного (А) и движущегося (В) источника

Получим количественные соотношения для эффекта Доплера в простейшем случае, когда источник колебаний и наблюдатель движутся вдоль одной и той же оси Х. Обозначим: V – скорость распространения волны, V_И и V_Н – скорости источника и наблюдателя в некоторой инерциальной системе отсчета. Источник I, находящийся в начале координат в момент времени =0 начинает излучать волны с частотой n₀.

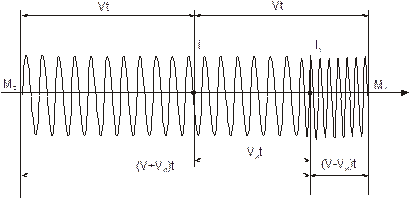
Рис. 1.21. К эффекту Доплера

Рассмотрим случай, когда источник движется в направлении оси Х со скоростью, удовлетворяющей условию V_И<V. Пусть за время t волновой фронт достиг точек М₁ и М₂ оси Х с координатами ±Vt. Предположим, что в точках М₁ и М₂ находятся неподвижные наблюдатели, измеряющие частоту приходящей волны. За время t источник переместится в положение I₁, с координатой V_Иt. При частоте колебаний источника n₀ за это время будет испущен цуг волн длиной (V-V_И)t в направлении оси Х и длиной (V+V_И)t в направлении, противоположном оси Х. Эти цуги содержат N=n₀t волн. Длина волны в направлении оси Х равна:

.

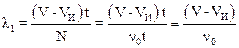Используя определение длины волны, запишем

.

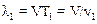Последнее соотношение позволяет найти частоту волны воспринимаемой наблюдателем в М₁:

.

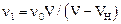Аналогичным образом получим частоту волны, регистрируемой наблюдателем, находящимся в точке М₂:

.

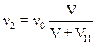Рассмотрим теперь случай, когда источник волн неподвижен, а наблюдатель М₁ приближается к источнику со скоростью V_H. Частота источника по-прежнему равна n₀. За время t мимо неподвижного наблюдателя прошел бы цуг волн длиной Vt, содержащий N=n₀t волн. В результате встречного движения наблюдатель зарегистрирует дополнительные волны укладывающиеся на пройденном им пути V_Нt. Число таких волн равно:

,

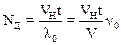здесь l₀ длина волны неподвижного источника.

Полное число зарегистрированных за время t волн будет равно:

.

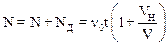Частота волны для такого наблюдателя равна:

.

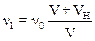Для наблюдателя удаляющегося от источника частота n₂ будет равна

.

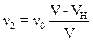Формулу для частоты волны, регистрируемой при совместном движении наблюдателя и источника можно получить, если в соотношениях (1.84) и (1.85) вместо n₀ использовать значения частоты, определяемые формулами (1.86) и (1.87):

.

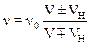Верхний знак необходимо записывать, если источник и наблюдатель приближаются друг к другу, нижний – когда удаляются.