Классический законсложения скоростей

Пусть некоторая система К' (X',Y',Z',O') движется равномерно и прямолинейно относительно другой, неподвижной системы К (X,Y,Z,O), со скоростью V₀.

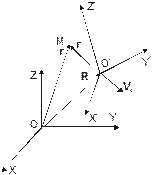
Рис. 2.1 . К преобразованию скоростей.

Как видно из рисунка 2.1, справедливо равенство:

,

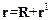где r – радиус-вектор точки М в неподвижной системе отсчета, r^I – радиус-вектор точки М в подвижной системе отсчета К' и R – радиус-вектор начала подвижной системы отсчета относительно неподвижной. Если предположить, что в начальный момент времени начала координат систем К и К^I совпадают, то вектор R=V₀t.

С учетом последнего замечания дифференцирование (2.2) по времени дает

.

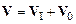Формула (2.3) – математическое выражение классического закона сложения скоростей, где V – скорость материальной точки М относительно неподвижной СО, V_I – скорость точки М относительно подвижной СО и V₀ – скорость подвижной СО относительно неподвижной.

В проекциях на оси координат X, Y, Z (2.3) записывается так:

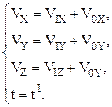
Последнее уравнение системы выражает представление об абсолютном времени, которое течет равномерно и одинаково во всех инерциальных системах отсчета.