КЛАССИЧЕСКИЙ АНАЛИЗ РОДСТВЕННЫХ КОРРЕЛЯЦИЙ
Сходство родственников, принадлежащих к разным поколениям (предки — потомки), обычно оценивается коэффициентом корреляции Пирсона, который называют также межклассовым коэффициентом корреляции. В случае близнецов и сиблингов применяется коэффициент внутриклассовой корреляции, подсчитываемый на основе дисперсионного анализа:
где х1' и х1j — значения одного и того же признака у близнецов одной пары.
Использование внутриклассовой корреляции в данном случае обусловлено тем, что нет генетического критерия для отнесения того или иного члена пары в тот или другой вариационный ряд. В табл. 8.4 приведен пример вычисления внутриклассовой корреляции для МЗ близнецов.
Таблица 8.4 Вычисление внутриклассового коэффициента корреляции
| Значение признака | х1 - х2 | (х1 - х2) | х1+ х2 | (х1 + х2) | ||
| Пары | близнец 1 х1 | близнец | ||||
| 2 i 4 | 4 i | 2 1 i | -2 1 1 | 4 1 1 | J | 25 9 |
| СУММЫ 11 41 439 |
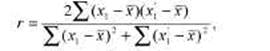
W = 11/2/5 = 1,1; 5 = {[439-41/5]/2/4-1,1}/2 = {[439-1681/5]/8-1,1}/2 =
= 5,875 R = 5,875 /(5,875 +1,1) = 0,842.
Внутриклассовый коэффициент корреляции, в отличие от межклассового, не изменяется при перемене мест членов пары.
При подсчете коэффициента корреляции обычно вычисляется и ошибка его измерения. Это важно, так как наличие ошибок измерения ведет к искажению коэффициента корреляции и, следовательно, при проведении генетического анализа по коэффициентам корреляции между родственниками будут получаться смещенные оценки компонентов дисперсии признака. В связи с этим производится поправка коэффициентов корреляции на дисперсию ошибки измерения, для чего проводят повторные измерения признаков у одних и тех же индивидов. Дисперсия ошибки измерения равна внутрипарной дисперсии (V0 = W), вычисленной по повторным измерениям. Когда дисперсия ошибки подсчитана, коррекция межклассовых коэффициентов корреляции осуществляется с использованием следующей формулы:
R = R [1+Ve1 /(S12 - Ve1 )][1+Ve2 /(S22 - Ve2)],
где Я — исходный коэффициент корреляции между первыми и вторыми родственниками по изучаемому признаку: Sb S2 — дисперсии признака у соответствующих родственников.
Использование индексов 1-й (например, родители) и 2-й (например, дети) групп родственников обусловлено тем, что указанные группы могут отличаться друг от друга по изучаемым признакам вследствие половых, возрастных и тому подобных различий.
Коррекция коэффициентов внутриклассовой корреляции (между близнецами, сиблингами) на дисперсию ошибки измерения проводится по формуле:
R = B/(B + W-Ve)
где В — межпарная дисперсия, W— внутрипарная дисперсия. Если приведенные в табл. 8.5 данные рассматривать как повторные измерения одних и тех же индивидов, то дисперсия ошибки измерения VС = W = 1,1, а внутриклассовая корреляция в данном случае соответствует коэффициенту воспроизводимости.
Корреляции разных типов родственников несут в себе специфическую информацию о разных составляющих фенотипической дисперсии в популяции (табл. 8.5). Например, при изучении пары приемный родитель — усыновленный ребенок можно получить оценку вклада
13*
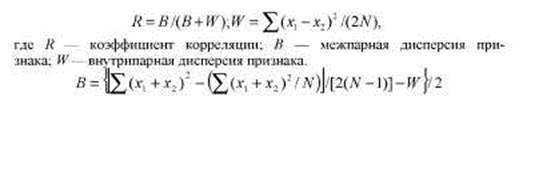
общей семейной и родительско-детской среды. При изучении же только корреляций биологических родителей и детей разделить составляющие генетической аддитивной дисперсии и родительско-детской среды невозможно, поскольку их объединяет и общая среда, и 50% общих генов. Этот метод применим только в сочетании по крайней мере с одним другим методом, который позволил бы разделить влияния генетических и средовых компонентов.
Таблица 8.5
Вклады аддитивного (Va), доминантного (Vd) и общего средового (VEC) компонентов фенотипической дисперсии в фенотипические корреляции разных типов родственников
| Типы родственников | VA | VD | Vec |
| Биологические родители и дети | 1/2 | Vc(bpo) | |
| Приемные родители и дети | VС(АРО) | ||
| Сиблинги с одним общим родителем | 1/4 | Cc(hs) | |
| Сиблинги | 1/2 | 1/4 | VС(FS) |
| Двуяйцевые близнецы | 1/2 | 1/4 | VC(DZ) |
| Однояйцевые близнецы | 1,0 | 1,0 | Vc(mz) |
Примечание. Здесь и далее:
ВРО — родители Х дети (biological parent-offspring); AP O — приемные родители Х дети (adopted parent-offspring); HS — полусиблинги (half-sibling); FS — полные сиблинги (full-sibling); DZ— ДЗ близнецы (dizygotic twins); MZ — МЗ близнецы (monozygotic twins).
С целью максимизации информации, полученной при анализе разных типов родственников, ученые совмещают несколько методов в рамках одного исследования. Выбор методов для исследования того или иного признака является специальной задачей. Главное правило здесь заключается в том, что количество независимых исходных статистик (т.е. количество корреляций между родственниками) должно превышать количество неизвестных в системе уравнений. Если это правило не выдерживается, система уравнений однозначного решения не имеет.
Например, представим себе, что мы исследуем по некоторому признаку биологические семьи, каждая из которых растит по крайней мере двух детей. Соответственно, мы можем определить корреляции по исследуемому признаку как между родителями и детьми, так и между сиблингами в данных семьях. Любая из этих пар будет иметь в среднем 50% общих генов, что позволяет, используя информацию из табл. 8.5, записать следующую систему уравнений:
ГВРО ~1 ' 2 * А ~"~ *С (ВРО) J ' " Р '
rFS ~Y ' 2 VA ' '4 V D +V C(FS) ] / V P .
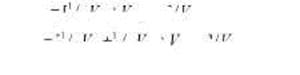
Чем больше различных пар родственников включено в анализ, тем больше компонентов дисперсии может быть определено однозначно и тем более сложные и разветвленные модели могут оцениваться.
В качестве иллюстрации рассмотрим два метода, используемых для разделения генетической и средовой составляющих фенотипической дисперсии в популяции (подробнее о методах психогенетики — в гл. VII).
Метод близнецов. Этот метод, без сомнения, был и до сих пор является одним из ведущих методов психогенетики. Классический вариант метода близнецов основывается на том, что монозиготные (МЗ) и дизиготные (ДЗ) близнецы характеризуются различной степенью генетического сходства, в то время как их среда может считаться приблизительно одинаковой. На языке составляющих фенотипической дисперсии (см. табл. 8.2 и 8.3) это можно выразить так:

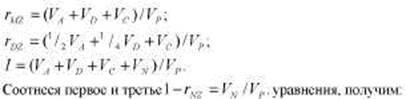
МЗ близнецы представляют собой идентичные генетические копии друг друга, поэтому теоретически корреляция МЗ близнецов по признаку, вариативность которого в популяции находится полностью под генетическим контролем, должна равняться 1,0. Разницу между 1,0 и реальной корреляцией МЗ близнецов можно объяснить влияниями индивидуальной среды или ошибки измерения (компонент Vn содержит в нерасчлененном виде обе эти составляющие).
Отметим, что приведенные закономерности соотношения МЗ и ДЗ близнецов справедливы только при следующих условиях (частично речь о них шла в гл. VII):
1. Центральным допущением при использовании метода близнецов в любом его варианте является допущение о равенстве среды МЗ и ДЗ близнецов. Важно отметить, что оно подразумевает не одинаковость близнецовых сред, а тот факт, что распределение (частота встречаемости и разброс) средовых компонентов монозиготных близнецов не превышает разнообразия сред дизиготных. Правомерность этого допущения до сих пор исследуется и обсуждается психогенетиками; если оно не справедливо, то получаемые этим методом оценки коэффициента наследуемости искажены. Как уже говорилось, это допущение касается не всей близнецовой среды, а только тех ее аспектов, которые связаны с изучаемым признаком (если они известны).
2. VgxЕ = 0, т.е. принимается допущение об отсутствии ГС-взаимодействия. Заметим, что в некоторых случаях такое допущение вполне правомерно, в большинстве же случаев оно требует тщательной эмпирической проверки.
3. Cov(g)(e) = 0, т.е. принимается допущение об отсутствии геyотип-средовой ковариации. Прямо проверить это допущение в рамках классического близнецового метода невозможно. Поэтому, как и в случае двух предыдущих допущений, отсутствие ГС-ковариации и корреляции при использовании классического метода близнецов принимается на веру.
4. Ассортативность по исследуемому признаку не отличается от нуля (т.е. ц. = 0). Как уже говорилось, это допущение для большинства исследуемых в психогенетике признаков неверно: неслучайность подбора супружеских пар у человека — скорее правило, чем исключение. Поэтому допущение об отсутствии ассортативности надо обязательно проверять (в том случае, если в литературе отсутствуют необходимые сведения) по данным о супружеских парах. В общем случае корреляция между супругами включает в себя компонент, обусловленный ассортативностью брака, и компонент, обусловленный влиянием семейных систематических средовых факторов. Самым простым и надежным способом проверки этого допущения является обследование родителей близнецов. Не имея данных о родителях (т.е. корреляций между родителями по исследуемому признаку), исследователь не может «развести» эффекты ассортативности и эффекты семейной среды. Наличие же значимой ассортативности повышает возможность получения ДЗ одинаковых генов от обоих родителей (у МЗ и без этого фактора их 100%), повышая rДЗ и тем самым снижая разность rМЗ - rДЗ и, следовательно, величину коэффициента наследуемости (о нем речь пойдет ниже).
5. В генетическом механизме изучаемого признака отсутствуют эпи-статические взаимодействия (Vt). Это условие принимается как должное практически во всех психологических исследованиях (многие исследователи принимают данное допущение a priori, даже не обсуждая его правомерность). Однако в ситуациях, когда это допущение не-
справедливо, оценки составляющих фенотипической дисперсии могут быть сильно искажены, поскольку эпистатическое взаимодействие генов может значительно уменьшить генетическое сходство ДЗ близнецов, тем самым увеличивая разницу между rМЗ и rДЗ и приводя к завышенным оценкам коэффициента наследуемости.
Однако даже в том (весьма неправдоподобном!) случае, когда исследуется психологический признак, для которого соблюдаются все вышеперечисленные условия, оценить все четыре компонента фенотипической дисперсии (VA,Vd ,Vc ,VN ) в рамках метода близнецов невозможно, так как четыре независимых величины не могут быть определены из трех линейных уравнений. Ученые, тем не менее, сделав несколько упрощающих допущений, разработали несколько способов оценки коэффициента наследуемости на основе метода близнецов. Отметим, что ни один из этих методов не является «правильным» или «неправильным» — каждый из них обладает определенными достоинствами и недостатками. Рассмотрим кратко хотя бы три наиболее часто встречающихся в литературе метода оценки коэффициента наследуемости.
КОЭФФИЦИЕНТ ХОЛЬЦИНГЕРА
К. Хольцингер предложил следующую формулу для оценки наследуемости:
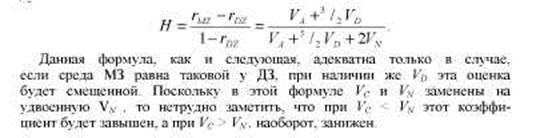
КОЭФФИЦИЕНТ ИГНАТЬЕВА*
В качестве первой оценки величины генетической составляющей фенотипической дисперсии часто используется коэффициент Игнатьева, вычисляемый следующим образом:
* Данный способ оценки генетического компонента дисперсии и зарубежной психогенетике связан с именем Д. Фальконера, работа которого вышла в I960 г. Однако этот коэффициент был предложен еще в 1934 г. М.В. Игнатьевым. Кратко об этом см. во Введении, а также в работах В.М. Гиндилиса [97] и Б.И. Кочубея [132, гл. I]. В формуле Игнатьева используются иные символы, но, поскольку в современной науке утвердились приводимые далее обозначения, будем пользоваться ими и мы. В приводимой ниже формуле Еобщ — то же, что ЕС, a Eинд — то же, что EN в предыдущем тексте (см. табл. 8.3).
При наличии доминантного компонента дисперсии VD оценка наследуемости будет завышена.
Очевидно, что влияние любых факторов, изменяющих разницу между корреляциями двух типов близнецов (например, завышение корреляции между МЗ близнецами, возникающее в результате действия специфической для этого типа близнецов среды), будет влиять на эту оценку наследуемости. Хотя в последние годы появились и все чаще употребляются более современные и сложные методы статистического анализа, этот коэффициент, в силу своей аргументированности и простоты получения, остается в арсенале психогенетики. Более того, Р. Пломин предложил с помощью этой формулы оценивать — тоже в первом приближении, конечно, — и долю средовых компонентов:
где С — значение со-близнеца по исследуемому признаку (данный метод подразумевает выделение в каждой паре одного близнеца — условного пробанда, тогда второй близнец называется со-близнецом); Р — значение близнеца-пробанда по тому же признаку; R — коэффициент родства (1 для МЗ и 0,5 для ДЗ близнецов); PR — произведение
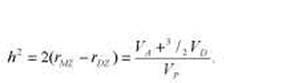

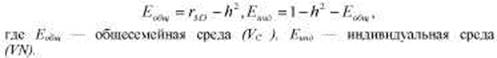
Правда, в оценку индивидуальной среды неизбежно включается часть дисперсии, вызванная ошибкой измерения. Возможность коррекции этого дефекта обсуждена выше.
МЕТОД ДЕ ФРИЗА И ФУЛКЕРА (ДФ-МЕТОД)
Дж. де Фриз и Д. Фулкер разработали две регрессионные модели: 1) классическую регрессионную модель, в которой частная регрессия значения со-близнеца на значение близнеца—условного пробанда и коэффициент родства представляет собой тест генетической этиологии исследуемого признака, и 2) расширенную регрессионную модель, предоставляющую прямое свидетельство того, насколько индивидуальные различия внутри исследуемой группы объясняются генетическими и средовыми влияниями. Эти два регрессионных уравнения записываются следующим образом:
значения пробанда по исследуемому признаку на коэффициент родства; А — константа регрессионного уравнения.
Решение этих уравнений позволяет оценить следующие параметры: Вь представляет собой показатель среднего сходства между МЗ и ДЗ близнецами; В2 — оценку удвоенной разницы между средними в группах МЗ и ДЗ близнецов (с учетом ковариации между значениями МЗ и ДЗ пробандов); В3 оценивает долю дисперсии, объясняемую сре-довыми влияниями, общими для членов близнецовой пары (VС /VР или С ); В4, отражает разницу h g - h2 , где h2 — коэффициент наследуемости в широком смысле и h g — коэффициент наследуемости в определенной группе (например, коэффициенты наследуемости IQ в группах здоровых людей и людей, страдающих ФКУ, отличаются друг от друга; В4 показывает разницу коэффициентов наследуемости, полученных в генеральной популяции и специфической выборке); и, наконец, В5 оценивает коэффициент наследуемости (h ), т. е. показатель того, насколько индивидуальные различия в исследуемой выборке объясняются наследуемыми влияниями.
Интересной особенностью ДФ-метода является то, что он позволяет тестировать гипотезу о сходстве или различии этиологии нормально распределенных и экстремальных значений. Сравнение регрессионных коэффициентов В2 и В5 позволяет проверить гипотезу о том, сходны ли этиологии девиантных и «средних» значений, например, по тесту на математические способности. Если этиология неспособности к математике отличается от этиологии средних математических способностей, то В2 и В5 должны статистически надежно отличаться друг от друга. Если же дети, которые имеют трудности в овладении математикой, представляют собой не отдельную группу, а край нормального распределения, то В2 и В5 статистически отличаться друг от друга не должны,
Разные формулы для вычисления коэффициентов наследуемости характеризуются разного рода допущениями и ограничениями. В нескольких исследованиях было продемонстрировано, что применение разных формул на одном и том же эмпирическом материале дает разные результаты. Поэтому интерпретация данных, полученных одним методом близнецов, должна проводиться с учетом всех ограничений, свойственных этому методу. Ф. Фогель и А. Мотульски [159] отмечают, что даже при сильно упрощающих допущениях (например, отсутствия ассортативности, доминирования и т.д.) все равно остаются систематические ошибки, которые невозможно полностью проконтролировать. Они рекомендуют вычислять из одних и тех же эмпирических данных альтернативные оценки и сравнивать, насколько хорошо они совпадают.
Метод приемных детей. При допущении, что среда семей-усыновителей не коррелирует со средой тех биологических семей, из которых данные дети усыновляются, корреляции детей с их биологичес-
кими родителями представляют собой «чистые» генетические корреляции (т.е. прямую оценку h2 или VG /VP, а с родителями-усыновителями — «чистые» средовые корреляции (с2 или VС /VP). Однако в том случае, если среды биологических и приемных семей похожи, допущение о «чистоте» полученных оценок генетической и средовой составляющих чаще всего неправомерно (по крайней мере в тех случаях, когда корреляция сред неизвестна). Методологически адекватным, хотя практически и не всегда возможным решением в подобной ситуации служит получение нескольких оценок генетического и средово-го компонентов при разных значениях корреляции сред.
Таким образом, главной причиной беспокойства при использовании метода приемных детей является допущение об отсутствии корреляции между биологическими и приемными семьями. Кроме того, исследователи должны убедиться в том, что семьи-усыновители репрезентативны общей популяции, т.е. не отличаются от среднепопуля-ционной семьи по уровню благосостояния, образования и т.п. Если семьи-усыновители нерепрезентативны, закономерности, полученные в результате их анализа, не могут считаться справедливыми для генеральной популяции.
АНАЛИЗ ПУТЕЙ
Приведенная выше логика разложения фенотипической дисперсии на ее составляющие, реализованная в нескольких эмпирических методах, представляет собой один из способов определения коэффициента наследуемости того или иного признака. Но понятие наследуемости можно также проанализировать при помощи «анализа путей».
Анализ путей в последние десятилетия широко используется и в психогенетике, и в науках о поведении вообще. Он был предложен генетиком С, Райтом еще в 30-х годах и затем им же и другими исследователями детально разработан. Четкое изложение его основ и правил использования содержится в упоминавшемся труде М. Нила и Л. Кардона [342], которые характеризуют этот метод следующим образом.
Диаграмма путей — эвристичный способ наглядного графического представления причинных и корреляционных связей (путей) между переменными, позволяющий дать полное математическое описание линейной модели, которую применяют исследователи. Тем самым диаграмма путей способствует ее пониманию, верификации или представлению результатов. В целом путевые модели — «экстремально обобщенный» способ анализа, один из многих мультивариативных методов (к ним же относятся методы множественной регрессии, факторный и дискриминантный анализы и т.д.).
Существуют определенные правила построения диаграмм путей (рис. 8.4). Прямоугольники (или квадраты) обозначают наблюда-
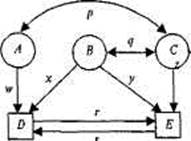
Рис. 8.4. Диаграмма путей, объединяющая три латентных (А, В, С) и две наблюдаемых (D и Е) переменных.
риq — корреляции; r, s, w, х, у, z — путевые коэффициенты.
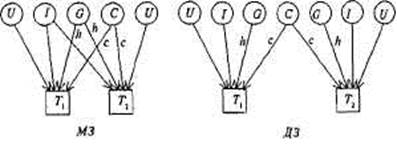
Рис. 8.5. Диаграмма путей для корреляций совместно живущих пар МЗ и ДЗ близнецов.
Th т2 — близнецы одной пары. G — генотип; С— общая среда; U — индивидуальная (уникальная) среда; I— эпистаз. Пути h, с — влияния G, С на исследуемую черту.
емые переменные; круги (или эллипсы) — латентные, неизмеряе-мые переменные (на рис. 8.4. D и Е; А, В, С соответственно).
Связи между переменными обозначаются стрелками: постулированные исследователем причинно-следственные — направленной в одну сторону («путь» от причины к следствию); наблюдаемые ассоциации — двусторонней. На рис. 8.4 первые — w, x, у, z, r, s (путевые коэффициенты); вторые — р и q (коэффициенты корреляции). Иначе говоря, модель выделяет зависимые переменные (D и Е), подлежащие объяснению или прогнозированию, и независимые (А, В, С), действие которых должно объяснить или предсказать зависимые переменные и их связи. Есть и другие, более детальные, правила оформления и чтения путевых диаграмм, но мы их рассматривать не будем.
На рис. 8.5 даны модели путей для корреляций совместно живущих пар МЗ и ДЗ близнецов по экстраверсии, из которых следует, что
корреляция МЗ близнецов T1 и Т2 может быть выражена через сумму путей, связывающих их, т.е. hh и сс; иначе говоря, rМЗ = h2 +с2 . Для ДЗ это будут пути h х 1/2 х h и cc, т.е. rДЗ = 1/2 h2 + с2 . Вычитая, получим rМЗ — rДЗ = h2 + с2 — 1/2 h2 — с2 = 1/2 h ; чтобы получить полную генетическую дисперсию (а не половину ее), удваиваем разность корреляций h2 = 2(rMЗ — rДЗ ) и получаем описанный выше коэффициент наследуемости, справедливый для близнецовых исследований. Аналогичным образом могут быть построены путевые диаграммы для семейных и любых других данных.
Единицы измерения, используемые в анализе путей, отличаются от тех, которыми мы оперировали тогда, когда рассматривали понятие наследуемости на примере разложения фенотипической дисперсии. Если при разложении дисперсии мы пользовались квадратичными единицами (например, h2 , VG ), то в данном случае наследуемость описывается на языке стандартных отклонений. Тогда путевые коэффициенты являются коэффициентами регрессии, полученными для переменных не в исходных единицах, а для стандартизованных переменных.
Несмотря на широкое использование этого метода и его достоинства, которые заключаются прежде всего в наглядной демонстрации представлений о компонентах, влияющих на исследуемый признак, он имеет и своих критиков. Так, Ф. Фогель и А. Мотульски «не уверены в том, что этот метод биометрического анализа внесет существенный вклад в наше понимание генетических факторов» [159]. Одно из главных сомнений вызывает тот факт, что в диаграмму путей и, следовательно, в дальнейший математический анализ закладываются уже имеющиеся у исследователя предположения о влияющих на признак факторах, их причинно-следственных отношениях и т.д., и результат анализа зависит, таким образом, от корректности заранее имеющихся исходных позиций.
АНАЛИЗ МНОЖЕСТВЕННЫХ ПЕРЕМЕННЫХ
До сих пор наши рассуждения концентрировались в основном на одном фенотипе, т.е. нашей конечной переменной являлся какой-то конкретно взятый фенотип. А если мы заинтересованы в одновременном изучении двух фенотипов, которые теоретически могут быть связаны между собой? Например, связана ли вариативность в популяции по таким высоко коррелирующим признакам, как вербальный и невербальный интеллект? Насколько вероятно предположение о том, что вариативность по этим двум признакам может быть объяснена действием одних и тех же генетических и средовых влияний? Иными словами, если два признака коррелируют на фенотипическом уровне, то эта корреляция может быть результатом действия как генетичес-
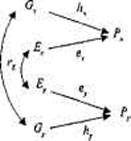
Рис. 8.6. Диаграмма путей фенотипической корреляции двух признаков Рх и Ру , демонстрирующая роль генетической rG и средовой rE составляющих.
ких, так и средовых факторов, и задача может заключаться в том, чтобы понять происхождение не только самих фенотипов, но и их корреляции.
Среди генетических причин, которые могут привести к появлению корреляции между признаками на фенотипическом уровне, следует указать на так называемый эффект плейотропии, или множественного влияния одних и тех же генов на разные признаки. Кроме того, различные популяционные процессы, например неслучайное скрещивание и смешивание популяций, также могут привести к возникновению корреляции между фенотипами.
Примером средового влияния на формирование фенотипической корреляции может служить дефицит питания: недоедающие дети обычно значительно ниже своих сверстников как по весу, так и по росту, т.е. связь этих двух характеристик обеспечивается одним средовым фактором.
Значимость такого рода одновременного моделирования множественных переменных трудно переоценить. Существуют целые классы поведенческих признаков, которые высоко коррелируют между собой (например, различные показатели когнитивной сферы, показатели эмоционально-волевой сферы и т.п.). Предположение о том, что вариативность по высоко коррелирующим психологическим признакам может объясняться действием одних и тех же генетических и/или средовых факторов кажется весьма правдоподобным.
Математическое описание множественных моделей достаточно просто, Рис. 8.6 представляет собой иллюстрацию того, как модель путей, рассмотренная нами, может быть разработана для одновременного анализа двух коррелирующих признаков. Подобно тому как фенотипическая вариативность отдельно взятого признака (Рх ) отражает вариативность генотипов (hх ) и сред (ex), фенотипическая корреляция между X и Y (rРх Ру ) может быть результатом набора генетических (hx hу rG) и средовых (ех еy RЕ) путей, где rG и rЕ представляют
собой генетическую и средовую корреляции, соответственно. В результате
rPxPf = hx hy r G + ех еy RЕ
ОЦЕНКА СОСТАВЛЯЮЩИХ ФЕНОТИПИЧЕСКОЙ ДИСПЕРСИИ МЕТОДОМ ПЕРЕБОРА (ПОДБОРА) МОДЕЛЕЙ(МПМ)
Некоторые корреляции родственников (например, корреляции МЗ близнецов, разлученных при рождении, или приемных сиблингов — усыновленных детей-неродственников, выросших в одном доме) сами по себе дают информацию, которой достаточно для получения ответов на центральные вопросы психогенетики о том, насколько вариативность данного признака объясняется разнообразием сред и генотипов, наблюдаемых в данной популяции. Подобное может быть сказано и о тех методах психогенетики, которые сопоставляют корреляции, полученные у двух типов родственников, например корреляции МЗ и ДЗ близнецов, приемных детей — с биологическими и приемными семьями.
Однако в современных исследованиях предпочтение при анализе психогенетических данных отдается не прямым оценкам составляющих фенотипической дисперсии, а применению метода перебора (подбора) моделей. Этот метод представляет собой специфическую адаптацию метода структурного моделирования к задачам генетики количественных признаков. МПМ отличается несколькими преимуществами: 1) более точной оценкой искомых параметров; 2) возможностью оценивать более сложные генетические модели, например учитывать половые различия и моделировать ГС-корреляции и в-заимодействия; 3) возможностью сводить в одном анализе данные, относящиеся к разным типам родственников, и получать, благодаря этому, относительно несмещенные оценки параметров и 4) возможностью тестирования нескольких альтернативных моделей с целью выбора той, которая наилучшим образом соответствует исходным данным.
В рамках генетики количественных признаков применение метода перебора моделей сводится к решению систем уравнений для обнаружения такого набора параметров (т.е. подбора такой модели), который наилучшим образом соответствует набору исходных данных (корреляций родственников). Главное преимущество МПМ заключается в том, что он позволяет тестировать все те допущения, которые не учитываются в традиционных методах генетики количественных признаков. Например, обсуждая метод близнецов, мы указывали на то, что одним из допущений этого метода является допущение об отсутствии ассортативности. МПМ позволяет сравнить две модели (учитывающую ассортативность и не учитываю-
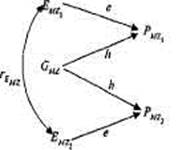
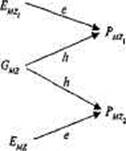
Рис. 8.7. Диаграмма путей фенотипических корреляций по исследуемому признаку для двух типов МЗ близнецов: (а) выросших вместе и (6) разлученных при рождении [по: 364].
Обозначения — в тексте.
щую ее) и выбрать ту, которая наилучшим образом соответствует эмпирическим данным.
В качестве еще одного примера применения МПМ рассмотрим анализ родственных корреляций на основе модели, приведенной на рис. 8.7. Эта модель описывает фенотипическое сходство МЗ двух типов — выросших вместе (а) и разлученных при рождении (б). Каждая из моделей содержит: две измеряемых переменных — фе-нотипические значения близнецов, PMZ1 и РМZ2 ), и две латентных, неизмеряемых переменных — эффекты генотипа (G), и эффекты среды (Е). Среды близнецов, выросших вместе, коррелируют rE MZ . Путь от латентной переменной — генотипа (G) к измеряемой переменной — фенотипу (Р) обозначается h; путь от латентной переменной среды (Е) к измеряемой переменной фенотипа (Р) обозначается е. Задача моделирования заключается в том, чтобы решить систему уравнений и оценить два неизвестных параметра — е и h. Применяя правила анализа путей, запишем следующую систему уравнений:
(6)rMZ=hxh = h2.
Эта система содержит два уравнения и два неизвестных и решается алгебраически.
Итак, мы проиллюстрировали простое приложение МПМ. На первом этапе с помощью диаграмм путей записывается система уравнений, описывающих фенотипические корреляции для всех типов родственников, данные которых анализируются. Затем исследователь формулирует набор альтернативных моделей, среди которых и ведется поиск модели с наилучшим соответствием эмпирическим данным.
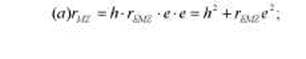
Например, исследователь может протестировать соответствие полученным данным следующих трех моделей, согласно которым феноти-пическое сходство родственников по определенному признаку объясняется: 1) только аддитивной генетической составляющей; 2) только доминантной генетической составляющей; 3) наличием и аддитивной, и доминантной генетических составляющих. Модель наилучшего соответствия выбирается на основе значения %-квадрата и других статистических показателей, оценивающих степени соответствия модели исходным данным.
Как уже указывалось, перебираемые модели могут быть очень разветвленными и сложными; они могут включать в себя множественные фенотипы, измеренные у нескольких типов родственников лонгитюд-ным методом (т.е. несколько раз за время исследования) и т.д.
Результаты применения МПМ могут быть использованы только при тестировании альтернативных моделей. Иными словами, МПМ не дает «доказательств» правильности тестируемой научной гипотезы; он позволяет лишь выбрать наиболее адекватную материалу генетическую модель. МПМ является элегантным и сложным статистическим методом, применение которого требует наличия определенных навыков*.
СТРУКТУРНОЕ МОДЕЛИРОВАНИЕ
Структурное моделирование —сложный современный метод, требующий и больших объемов выборок, и специальной квалификации исследователя, и наличия соответствующих компьютерных программ. Детальное изложение его не входит в задачи данного учебника, мы даем краткую характеристику его возможностей, чтобы читатель, столкнувшись в литературе с этим типом анализа, смог адекватно понять его смысл.
Статистические методы моделирования с помощью линейных структурных уравнений (МЛСУ)**, описывающих латентные переменные, были разработаны на основе приемов статистического анализа множественных переменных, используемых биологами, экономистами, психологами и социологами, МЛСУ предполагает формулирование набора гипотез о влиянии одних переменных (независимых) на другие (зависимые) переменные. Соответствие подобного набора гипотез, т.е. теоретической модели, и реальных данных, собранных при работе с конкретной выборкой, т.е. эмпирической модели, формализуется с помощью статистического алгоритма, оценивающего степень их согласованности (меру соответствия).
* Полное описание спецификации МПМ в рамках количественной генетики выходит за пределы данного учебника. Подробное изложение этого метода дается в руководствах Лоэлина [320J, а также Нила и Кардона 1342]. На русском языке пример применения МПМ в рамках психогенетики приведен в работе Е.А. Григоренко иМ. ЛаБуды 144].
** История возникновения и этапы детальной разработки МЛСУ описаны Бентлером [189; 190], а в работах Боллена [198] и Бентлера и его коллег [191] содержится современное техническое описание МЛСУ.
МЛСУ особенно полезно при статистическом анализе большого количества переменных, интеркорреляции которых известны. Задачами его являются: суммирование этих переменных, определение отношений между ними, оценка качества измерительных инструментов, контроль ошибки измерения (как для измеряемых, так и для латентных переменных) и нахождение соответствия между измеряемыми и латентными структурами. Правомерно будет сказать, что в ситуациях, когда набор переменных неточно измеряет латентную структуру, являющуюся предметом исследования, т.е. практически в любом случае, когда больше чем одна наблюдаемая переменная используется для представления латентной структуры, МЛСУ с латентными переменными следует применять как наиболее адекватный метод статистического анализа. Учитывая, что в психологии большинство латентных структур измеряется именно посредством не одной, а нескольких переменных и не может быть представлено без ошибки измерения, возможность и необходимость применения МЛСУ в этой области знаний становится очевидной.
Моделирование с помощью структурных уравнений представляет собой метод, родственный методу систем регрессионных уравнений, который используется при формулировании, детализации и тестировании теории или гипотезы. Структурные уравнения соотносят зависимые переменные и набор детерминирующих (независимых) переменных, которые в свою очередь могут выступать в роли зависимых переменных в других уравнениях. Подобные линейные уравнения в совокупности с уравнениями, детализирующими компоненты дисперсии и ковариации независимых переменных, составляют структурную модель. Составление и запись уравнений, детализирующих компоненты дисперсии и ковариации независимых переменных, осуществляются с помощью матричной алгебры.
Статистической основой МЛСУ является асимптотическая теория, подразумевающая, что оценка и тестирование моделей осуществляются при наличии относительно больших по численности выборок испытуемых. Использование МЛСУ требует больших затрат компьютерного времени, поэтому пользователи при тестировании моделей предпочитают использовать стандартные статистические пакеты типа LISREL [295] и EQS [189]. Эти пакеты, несмотря на различия в деталях, основаны на одних и тех же общих математических и статистических подходах, применяемых к анализу систем линейных структурных уравнений. Основополагающая математическая модель [189] относится к классу ковариационных структурных моделей, включающих как множественную регрессию, анализ путей, одновременный анализ уравнений, конфирма-торный факторный анализ, так и анализ структурных отношений между латентными переменными. Согласно модели Бентлера-Викса, параметры любой структурной модели могут быть представлены в виде регрессионных коэффициентов, дисперсий и ковариации независимых переменных. Статистическая теория позволяет оценивать эти параметры с использованием мульти-факторной нормальной теории, а также более общих теорий — эллиптической и арбитрального распределения, основываясь на обобщенном методе наименьших квадратов или теории минимального х-квадрата.
* * *
В данной главе мы рассмотрели несколько краеугольных понятий генетики количественных признаков. Ее центральным допущением является представление о том, что фенотипическая вариативность признака может быть представлена в виде независимо действующих
14-1432
генетической (аддитивной, доминантной и эпистатической) и средо-вой (общей и индивидуальной) составляющих и составляющей, описывающей взаимодействия между генами и средой (ГС-корреляции и ГС-взаимодействия). На этом строятся существующие в количественной генетике математические методы. Используя принцип разложения фенотипической дисперсии, можно определить так называемый коэффициент наследуемости, который говорит о том, какой процент фенотипической дисперсии объясняется вариативностью генотипа в популяции, Коэффициент наследуемости может быть определен несколькими способами, каждый из которых имеет свои достоинства и недостатки, поэтому использование того или иного способа должно определяться задачами работы, типом и объемом эмпирического материала. Одновременно генетико-математические методы позволяют надежно выделить доли дисперсии, определяемые различиями в общесемейной и индивидуальной среде. Надо лишь иметь в виду, что содержательный анализ любого средового компонента требует привлечения собственно психологических знаний и иногда специального подбора экспериментальных групп.
Помимо общесемейной и индивидуальной среды выделяется среда, специфичная для разных вариантов внутрисемейных диад, причем ее влияние на когнитивные способности различно в разных диадах. Общая тенденция такова: близнецовая среда > сиблинговая > ро-дительско-детская > двоюродных родственников; эти типы сред объясняют, соответственно, 35, 22, 20, 11% дисперсии [444]. При этом влияние общесемейной среды падает к подростковому возрасту и практически исчезает у взрослых.
Важно иметь в виду, что, как уже говорилось, речь идет о математическом выражении той доли межиндивидуальной вариативности, за которую ответствен данный тип средовых воздействий. Конкретное же психологическое содержание каждого средового компонента — дело специальных, скорее же собственно психологических исследований. Однако значимость сравнительных оценок средовых компонентов (которые можно получить только в психогенетическом исследовании) трудно переоценить: именно они должны указать психологу, где надо искать релевантные исследуемой черте средовые переменные (например, в особенностях общей или индивидуальной среды). В этом — один из продуктивных аспектов взаимодействия двух наук.
Глава X
ПСИХОГЕНЕТИЧЕСКИЕ ИССЛЕДОВАНИЯ ТЕМПЕРАМЕНТА
1. ЧТО ТАКОЕ ТЕМПЕРАМЕНТ?
К темпераменту традиционно относят формально-динамические характеристики поведения человека, «характеристики индивида со стороны динамических особенностей его психической деятельности, т.е. темпа, быстроты, ритма, интенсивности составляющих эту деятельность психических процессов и состояний» [118]. Черты темперамента определяют не столько то, что человек делает, сколько как он это делает, иначе говоря, они не характеризуют содержательную сторону психики (хотя, конечно, опосредованно влияют на нее).
Концепции темперамента весьма разнообразны. Начало его изучения обычно приписывают двум врачам — древнегреческому Гиппократу (V-IV вв. до н.э.) и древнеримскому Галену (II в. до н.э.). Описанные ими четыре основных темперамента (холерики, сангвиники, флегматики и меланхолики) существуют и в современных классификациях. По-видимому, древним ученым удалось выделить и описать очень существенные, удержавшиеся в течение веков типы чело-
веческого поведения. Однако они пытались не только описать внешние особенности поведения, но и найти их причину. В соответствии со взглядами того времени эти темпераменты связывались с разными сочетаниями основных «жидкостей» человеческого тела. Позднее неоднократно предпринимались попытки связать темперамент человека с его анатомией или физиологией, в том числе с индивидуальными особенностями функционирования центральной нервной системы. Обзор современных концепций темперамента, представлений о его структуре и экспериментальных подходов к его изучению дан в книге М.С.Егоровой [58].
Для психогенетического исследования существенны несколько моментов. Во-первых, в разных возрастах компонентный состав темперамента оказывается разным, поскольку некоторые особенности поведения, характерные для маленьких детей (например, регулярность отправления физиологических функций, длительность сна и т.п.), либо отсутствуют, либо имеют совсем иной смысл в более старших возрастах; во-вторых, методы диагностики динамических характеристик — вопросники, основанные на самооценке, экспертные оценки, проективные методики, наблюдение, как правило, имеют значительно меньшую, чем, например, тесты IQ, статистическую надежность и часто дают разные результаты; в-третьих, существует традиционная для психологии проблема соотношения темперамента и характера; хотя последний, в отличие от темперамента, часто связывается с содержательной стороной личности, это не позволяет надежно развести проявления одного и другого: динамические характеристики деятельности могут в конкретных случаях определяться не только чертами темперамента, но и, например, высокой мотивированностью к данной деятельности, т.е. собственно личностной чертой.
Вспомним, например, исследование ткачих-многостаночниц [74], в котором было показано, что высокая мотивация к труду, предъявляющему повышенные требования к темпу деятельности, способности быстро переключаться с одной операции на другую и т.д., компенсировала «природные» особенности, которые должны были осложнить продуктивную работу. Речь шла о подвижности нервных процессов (т.е. предположительно — об одном из факторов, определяющих темперамент); оказалось, что требуемый производством темп выполнения профессиональной деятельности выдерживали и «подвижные», и «инертные», но достигалось это за счет разного стиля выполнения производственного процесса. Он-то и компенсировал «природную» дефици-тарность темповых характеристик.
Соотношение темперамента и характера, в конечном счете, сводится к проблеме «индивид и личность». Если фенотипические признаки, характеризующие динамическую сторону поведения, могут быть продуктом и темперамента, и личностных установок, то как различать их? По-видимому, и здесь решающим может выступить «генетический аргумент»: понимая личность как системное образование, от-
ражающее социо-культурный контекст, общественные отношения, в которые включен человек, мы, очевидно, не можем относить к этому уровню в структуре индивидуальности наследственно заданные свойства. Они принадлежат индивидному уровню, объединяющему сложившиеся в эволюции и в индивидуальном развитии биологические, — в частности, кодированные в геноме, — характеристики индивидуальности. Поэтому правы А. Басе и Р. Пломин [222; см. также 132, гл. VIII; 58], включающие наследуемость в число критериев, обязательных для отнесения той или иной психологической черты к темпераменту.
Однако надо иметь в виду, что в зарубежной психологии практически нет традиции, разделяющей в структуре индивидуальности эти два уровня — индивид и личность. Поэтому в содержании вопросников, в других диагностических процедурах и в получаемых затем факторах и схемах описания индивидуальности в целом часто объединяются черты и свойства, которые отечественный психолог отнес бы к разным подструктурам индивидуальности.
Даже в тех случаях, когда эти два термина — темперамент (temperament) и личность (personality) разводятся, речь идет скорее об объемах понятий, чем о разных подструктурах или уровнях интегральной индивидуальности. Дж. Лоэ-лин, например, ставя вопрос о соотношениях этих двух терминов, пишет: «В основном мы будем использовать личность как более широкий термин, в то время как темперамент ограничивается такими аспектами личности, которые проще, раньше проявляются в онтогенезе, часто ассоциируются с эмоциональной экспрессией» [318; с. 4]. В качестве иллюстрации он использует следующее рассуждение: пугливость может быть характеристикой темперамента ребенка в возрасте 1 года; она же может быть характеристикой поведения человека 21 года; в тех пределах, в которых мы считаем, что эти две характеристики есть одно и то же, с более или менее прямой передачей в ряду лет, она может рассматриваться как черта темперамента и у 21-летнего человека. Однако у него пугливость, вероятно, впитала в себя дополнительные черты, отражающие предыдущий социальный опыт, удаляющий ее от первоисточника, от корней, что и заставляет обозначить ее более широким термином «личностная черта».
Подобная постановка вопроса правомерна, но, может быть, выделение генотипической составляющей в этом сплаве — личностной черте — и позволит отделить свойство темперамента от приобретенного опыта?
Трудности, связанные с проблемой «темперамент—характер», заставляют некоторых исследователей считать, что черты темперамента в чистом виде могут быть диагностированы только у младенцев, когда социальный опыт минимален. Наиболее полно возрастной аспект психогенетических исследований темперамента обобщен в упомянутой книге Дж. Лоэлина [318]. Дальнейшее изложение в основном — извлечения из этой книги.
2. ИССЛЕДОВАНИЕ ГЕНОТИП-СРЕДОВЫХ СООТНОШЕНИЙ В ИЗМЕНЧИВОСТИ КОМПОНЕНТОВ ТЕМПЕРАМЕНТА У ДЕТЕЙ ПЕРВЫХ ЛЕТ ЖИЗНИ
В исследовании М. Риза [по: 318], проведенном на 45-47 парах МЗ близнецов, 38-39 однополых парах и 70-82 парах разнополых ДЗ первых дней жизни (3,7 дня для доношенных и 46,9 дня для недоношенных или имевших медицинские проблемы, ликвидированные к моменту обследования), у тех и других получены одинаково низкие внут-рипарные корреляции по четырем чертам темперамента (возбудимость, способность успокаиваться и др.) и по характеристикам активности во сне и бодрствовании. Корреляции у МЗ близнецов колеблются в пределах 0,06-0,31, у однополых ДЗ они равны 0,06-0,59, у разнополых — 0,13-0,30. Автор полагает, что главной причиной этого являются пренатальные условия и особенности родов; аргументом в пользу такого объяснения служат корреляции между различиями по поведенческим характеристикам, с одной стороны, и весом при рождении и тесту Апгар, говорящему о физиологической зрелости новорожденного, — с другой. Как заключает Дж. Лоэлин, в этом возрасте гены не являются основным источником индивидуальных различий по темпераменту «или, точнее, еще не являются».
В ближайшие месяцы ситуация существенно меняется. В четырех исследованиях, проведенных с близнецами 10 возрастов — от 3 до 12 месяцев жизни (группы МЗ — от 29 до 117 пар, ДЗ — от 18 до 213 пар), использовавших разные методики оценки поведения детей — от лабораторных до наблюдения, только в одном случае сходство в парах ДЗ близнецов оказалось выше, чем МЗ; в остальных 9 возрастных группах корреляции МЗ выше, чем ДЗ. Коэффициент наследуемости, правда, пока невелик — в среднем около 30%, но генетические влияния уже вполне отчетливы.
Это подтверждается и методом приемных детей: в Колорадском исследовании биологические сиблинги (101 пара в возрасте 1 года) имели корреляцию по шкале Н. Бейли, оценивающей особенности поведения ребенка, равную 0,20, а у 83 пар приемных сиблингов она была практически нулевой (0,09). На следующем, втором, году жизни генотипические влияния еще более отчетливы. В Луизвилльском близнецовом исследовании (близнецы 1,5 и 2 лет, 30-83 пары МЗ и 28-50 пар ДЗ) при оценке поведения ребенка двумя разными методами коэффициенты наследуемости уже достаточно высоки: h2 = 0,42-0,56, что сопоставимо с величиной генетической детерминации экстраверсии и нейротицизма у взрослых.
По данным того же исследования, в течение первых двух лет МЗ близнецы оказываются более похожими и по возрастной динамике оценок, получаемых по шкалам темперамента и личности; усредненные по нескольким шкалам и возрастным этапам (в пределах 9-48 ме-
16-1432 241
сяцев) корреляции таковы: rмз = 0,50; rдз = 0,18. Это может говорить о том, что индивидуальные траектории развития на данном отрезке онтогенеза также испытывают влияние наследственности.
Э.Ф. Кириакиди [77] у близнецов 21-25 месяцев жизни (x = 23мес.) оценивала, среди прочего, особенности поведения по методике Н. Бейли (одна из наиболее распространенных и хорошо отработанных шкал для диагностики детского развития). Эта часть шкалы объединяется в три фактора, два из которых могут быть отнесены к категории темперамента: эмоциональность — экстраверсия и активность. Результаты показали, что на абсолютные оценки по этим факторам влияют конкретные особенности домашней среды: наличие в семье бабушки, систематические игры родителей с детьми, хорошие жилищные условия. Однако внутрипарное сходство и, следовательно, коэффициент наследуемости от этих обстоятельств не зависит. Генетический компонент обнаружился только в дисперсии оценок эмоциональности (0,30 и 0,47 при двух разных способах вычисления). Индивидуальные различия по активности полностью определяются средой, причем в обоих случаях большую роль играет индивидуальная среда. Но при этом эмоциональность и активность оказались связанными генетической корреляцией (rG = 0,45), что свидетельствует о наличии у них некоторой общей основы, общей системы генов, определяющих вариативность обеих черт.
Несколько иной подход к исследованию динамики поведения детей был реализован в Нью-Йоркском лонгитюдном исследовании, в котором были выделены 9 компонентов, описывающих динамику поведения ребенка: активность (главным образом двигательная), регулярность (ритмичность появления поведенческих реакций, например, проявлений голода, отправления физических функций, смены циклов сна и бодрствования и т.д.); приближение-удаление (иначе обозначается как реакция к/от: направление эмоционального и двигательного ответа на новые стимулы); адаптивность (реакция на новую ситуацию); интенсивность реакции любого знака; порог активности; доминирующее настроение; отвлекаемость (легкость изменения поведения в ответ на новые ситуации); внимание/настойчивость (длительность какой-либо деятельности и способность продолжать ее вопреки помехам). На основе Нью-Йоркского лонгитюдного исследования А. Торгерсен провела близнецовое исследование, результаты которого в табл. 10.1 [по: 132; гл. VIII].
Таким образом, уже начиная примерно с 9 месяцев жизни проявляется генетически заданная индивидуальность в сфере динамических характеристик поведения ребенка, т.е. темперамента.
Поданным, полученным в Нью-Йоркском лонгитюдном исследовании (оно началось в 1957 г.; первичная выборка— 133 ребенка раннего возраста), был выделен синдром трудного темперамента. Его признаками являются: низкая ритмичность, преобладание негативного настроения, слабая реакция «к», плохая адаптивность и высокая интенсивность реакций.
Оказалось, что этот синдром устойчив в первые годы жизни. В Нью-Йоркском исследовании в парах возрастов получены положительные корреля-
Таблица 10.1
Внутрипарное сходство МЗ и ДЗ близнецов в исследовании темперамента А. Торгерсен
| Показатели темперамента | Возраст | ||
| 2 месяца | 9 месяцев | 6 лет | |
| Активность | 1,52 | 5,26*** | 11,34*** |
| Регулярность | 4,98** | 12,86*** | 4 22*** |
| Приближение-удаление | 0,83 | 6,77** | 8,80*** |
| Адаптивность | 0,57 | 2,28* | 2,23* |
| Интенсивность | 2,55* | 5,32*** | 9 56*** |
| Порог реактивности | 2,82** | 9 ,90*** | 2 91*** |
| Настроение | 1,54 | 3 31** | 3,32** |
| Отвлекаемость | 1,40 | 3 94*** | — |
| Внимание-настойчивость | 4 40*** | 5, 13*** |
Примечание. Внутрипарное сходство МЗ и ДЗ близнецов оценивалось по соотношению дисперсий внутрипарных разностей. Значимое F-отношение говорит о большем сходстве МЗ по сравнению с ДЗ и, следовательно, о наличии генетического компонента в изменчивости признака.
*р < 0,05; **р < 0,01; ***р < 0,001
ции: 1 год и 2 года — 0,42; 2 и 3 года — 0,37; 3 и 4 года — 0,29; в Колорадском проекте аналогичные корреляции даже выше: 0,54, 0,61, 0,54 соответственно. Более того, начиная с трех лет обнаруживаются связи с темпераментом в период ранней взрослости (17-24 года): корреляции с оценками, полученными в 1 и 2 года, приближаются к нулю, но затем, в 3 и 4 года, они уже равны 0,31 и 0,37 (подумаем: ведь это интервал в 15-20 лет!).
Более того, трудный темперамент детства имеет проекцию в приспособленность взрослого человека к разным сферам деятельности — обучения, социальной, семейной и т.д.; соответствующие корреляции с первым и вторым годами жизни нулевые, но с трудным темпераментом в 3 года трудности взрослого уже имеют корреляцию r -0,21, а в 4 года r -0,32 (минус здесь означает, что, чем выше оценки трудного темперамента в детстве, т.е. чем он труднее, тем ниже приспособленность взрослого).
По данным упоминавшегося близнецового исследования А. Торгерсен, из пяти компонентов синдрома трудного темперамента в 6 лет три имеют высокую генетическую составляющую (слабая реакция «к», высокая интенсивность реакций, низкая регулярность: h2 = 0,94; 0,82; 0,68 соответственно), один — плохая адаптивность — определяется в основном общесемейной средой (с2 = 0,55), и еще один — негативное настроение — индивидуальной средой (е2 = 0,63). Правда, в двух последних признаках влияния наследственности тоже констатируются: h2 = 0,26 и 0,37 соответственно (см. [132; гл. VIII]).
16*
3. ИССЛЕДОВАНИЯ ЧЕРТ ТЕМПЕРАМЕНТА У ВЗРОСЛЫХ
В подавляющем большинстве работ используются схема и методики Г. Айзенка; оценивается экстра-интроверсия и нейротицизм или близкие к ним свойства: социабельность, активность и т.д. Меньше исследован психотицизм.
Напомним, что шкала экстраверсии объединяет такие характеристики, как социабельность, активность, оживленность, доминантность и т.п.; центральное ядро нейротицизма —эмоциональная стабильность-нестабильность, уровень эмоциональности в целом, но с ним коррелируют самооценка, осторожность и т.п. (однако это не клинический невротизм!); психотицизм, выделенный позже, характеризует агрессивность, холодность, эгоцентричность, отсутствие эмпатии и т.п. (но с ним коррелирует и креативность). На «низких» концах трех указанных суперфакторов индивидуальности располагаются: интроверсия, эмоциональная стабильность, Я-контроль [246,250].
Эти черты оказываются весьма стабильными в онтогенезе и по своей структуре, и по индивидуальной выраженности. Например, нейротицизм и социальная экстраверсия, оцененные у одних и тех же людей с интервалом в 45 лет, коррелируют на уровне 0,30 и 0,60, В другом лонгитюдном исследовании, охватившем людей от среднего возраста до старости, с интервалом в 30 лет, межвозрастная корреляция социальной интроверсии равна 0,74; по остальным шкалам (использовался MMPI) корреляции в среднем выше 0,40. Существуют и другие работы, выполненные разными диагностическими методами, на разных возрастных группах и интервалах, но говорящие о том же, а именно о возрастной стабильности этих характеристик индивидуальности [246].
Психогенетические исследования, суммированные Р. Пломиным с соавторами [364], показали отчетливое, хотя и не очень высокое влияние наследственности. В шведском исследовании (4987 пар МЗ близнецов и 7790 пар ДЗ 17-49 лет) получены такие оценки внутрипарно-го сходства: по экстраверсии rМЗ = 0,51 и rдз = 0,21, по нейротицизму оно такое же: 0,50 и 0,23 соответственно. Отсюда наследуемость в обоих случаях равна 0,5-0,6. Важно, что примерно те же оценки получены в независимом исследовании, проведенном в Австралии: внутри-парные корреляции МЗ и ДЗ близнецов (всего 2903 пары) по экcтpaверсии равны 0,52 и 0,17, по нейротицизму 0,50 и 0,23. Коэффициент наследуемости по экстраверсии выше, по нейротицизму примерно тот же, что свидетельствует о хорошей воспроизводимости результатов. В некоторых работах получено очень низкое сходство ДЗ близнецов — более чем вдвое ниже сходства МЗ, что говорит, по-видимому, о неаддитивном типе наследования. У разлученных МЗ (95 пар) и разлученных ДЗ близнецов (220 пар) сходство по экстраверсии выражается коэффициентами 0,30 и 0,04 и по нейротицизму 0,24 и 0,28 соответственно.
Обобщенные оценки наследуемости, полученные объединением различных близнецовых работ, дают около 40% генетической вариативности для экстраверсии и около 30% — для нейротицизма [364].
Более полно относящиеся к этим характеристикам данные проанализированы в упомянутой книге Дж. Лоэлина [318]. Вот некоторые из них.
В табл. 10.2 и 10.3 приведены результаты четырех исследований разлученных близнецов: финского, шведского, британского, Мин-несотского (США). В трех первых большинство близнецов были разлучены на первом году жизни, но некоторые пары — лишь после 10 лет; в Миннесотской выборке разлучение произошло в возрасте менее 3 мес, и длилось не менее 5 лет. Во всех группах некоторые пары имели контакты уже после разлучения, некоторые вновь объединились перед самым тестированием. Однако в любом случае это — близнецы, которые значительную часть своего детства провели в разных домах, т.е. в разной среде, и потому их сопоставление с выросшими совместно близнецами вполне информативно.
Таблица 10.2
Дата добавления: 2015-07-18; просмотров: 2094;
