Оценкинаследуемости особенностей взаимодействиямежду родителями и подростками,полученные методами наблюдения 4 страница
Приведем пример. Предположим, что известны гены, которые влияют на вес человека. Предположим также, что нормальный вес женщин среднего роста составляет 48-70 кг, т.е. разница между максимальным и минимальным значениями по весу равна 22 кг. Теперь предположим, что гены, контролирующие вариативность веса человека, расположены на каждой из 22 аутосомных хромосом (по одному на каждой), причем все гены вызывают примерно одинаковые эффекты. Тогда в рамках нашей гипотетической системы гомозиготы по каждому из изучаемых генов вкладывают примерно ± 1/2 кг (от средней точки), в зависимости оттого, являются они гомозиготами по аллелям, обозначаемым заглавной буквой (АА, ВВ, СС и т.д. - обладание этими генотипами повышает рост), или гомозиготами по аллелям, обозначаемым строчными буквами (аа, bb, ее и т.д. - обладание этими генотипами понижает рост). Рассмотренный пример, однако, невероятен по крайней мере по двум причинам: во-первых, генов, контролирующих вариативность веса человека, мы не знаем и, во-вторых, в реальной ситуации вклады генотипов, скорее всего, будут меньше или больше, чем 1/2 кг, затрудняя подсчет генотипического значения.
Модели генетики количественных признаков, во всяком случае в их классическом варианте, не являются ни средством идентификации конкретных генов, контролирующих вариативность признака, ни средством точного определения вклада каждого генотипа. Эти модели решают другую задачу, а именно задачу определения общего вклада генотипа в вариативность изучаемого признака в популяции.
Аддитивное генотипическое значение. «Аддитивное генотипическое значение» представляет собой фундаментальное понятие количественной генетики, поскольку оно отражает, насколько генотип «истинно наследуется». Аддитивный (суммарный) эффект генов представляет собой не что иное, как сумму эффектов отдельных аллелей. Более точно, аддитивное генотипическое значение есть генотипическое значение, обусловленное действием отдельных аллелей данного локуса. Генная доза генотипа подсчитывается на основе того, сколько аллелей определенного типа (например, аллелей А) присутствует в данном генотипе. Если наличие определенного аллеля в генотипе увеличивается на 1 (как это происходит, например, в случае перехода от генотипа аа к генотипу Aа), то аддитивное значение увеличивается на некоторую определенную величину. На рис. 8.2 дана графическая иллюстрация аддитивного генотипического значения при отсутствии доминантности. Эффект генотипа аа = -d, поэтому эффект аллеля (гена) а = 1/2(—d); эффект генотипа АА = d, поэтому эффект аллеля А = 1/2(d); соответственно, эффект генотипа Аа = 1/2(d) + 1/2(-d) = 0. Заметим, что аддитивные генные значения зависят от частоты встречаемости аллелей в популяции. При отсутствии доминирования аддитивный эффект полностью определяет генотипическое значение. Доминантность, однако, вносит самые разные отклонения от ожидаемых значений, — об этом пойдет речь ниже.
Теперь допустим, что каждый аллель генотипа имеет некоторый средний эффект. В этом смысле аддитивное генотипическое значение
представляет собой сумму средних эффектов каждого аллеля для всех аллелей, входящих в гено-' тип. Каждый аллель характеризу-
' ется определенным аддитивным
1 эффектом, соответственно, при
t унаследовании определенного ал-
\ леля от родителя ребенок насле-
j дует и аддитивный эффект этого
j____^_ аллеля, т.е. вклад аллеля в генотип ребенка будет таким же, ка-
Рис. 8.2. При отсутствии доминант- ким был его (аллеля) вклад в ге-
ности (h = 0) аддитивное генотипи нотип родителя. И неважно,
ческое значение определяется генной сколько (много или мало) алле-
дозой. лей присутствует в данном локу-
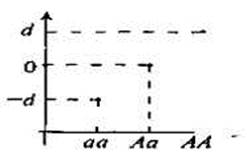
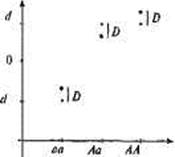
Рис. 8.3. Графическое изображение доминантных отклонений.
Наличие доминантности вносит разного рода изменения в аддитивное гепотипи-ческое значение.
Обозначения: • — аддитивные генотипические значения при условии полной доминантности; * — наблюдаемые аддитивные значения, определяемые на основе генных доз; D — доминантные отклонения, которые представляют собой разницу между ожидаемыми аддитивными значениями, соответствующими ситуации полной доминантности, и значениями, наблюдаемыми для определенных генных доз.
се или сколько локусов вовлечено в контроль вариативности по тому или другому признаку. Иными словами, аддитивное генотипическое значение представляет собой не что иное, как сумму вкладов каждого аллеля в генотип.
Доминантные отклонения. Доминантные отклонения есть мера того, насколько генотип отличается от своего ожидаемого аддитивного значения.
Доминантные отклонения (рис. 8.3) — это разница между ожидаемыми и наблюдаемыми значениями генотипов. Феномен доминантности допускает, что два аллеля одного локуса могут взаимодействовать друг с другом и тем самым менять генотипическое значение, которое наблюдалось бы в том случае, если бы они были независимы друг от друга и делали независимые вклады в генотипическое значение. Так, в результате взаимодействия аллелей Аа наблюдаемое генотипическое значение меньше того, которое ожидалось бы при условии полной доминантности. Напротив, значения АА и аа выше ожидаемых при допущении, что аллель А полностью доминантен по отношению к аллелю а.
Доминантность обязана своим возникновением уникальному сочетанию аллелей в данном локусе. Очевидно, что генотип потомка, наследующего только один аллель от каждого из родителей, в подавляющем большинстве случаев не может воспроизвести уникальность генотипа одного из них. Поэтому потомки будут отличаться от своих родителей в той мере, в какой аллели данного локуса не суммируются линейным образом при определении генотипического значения.
Рассмотрев типы генетических влияний, определим, как частоты встречаемости аллелей, определяющие эти типы, задают среднее значение генотипа в популяции. Допустим, что в популяции аллели А и а встречаются с частотами р и q, соответственно. Тогда первая колонка в табл. 8.1 показывает три возможных генотипа, вторая — частоты их встречаемости в популяции (при допущении, что особи в этой популяции образуют родительские пары случайным образом) и третья — значение генотипа. Популяционное среднее получается путем умножения значений генотипа на частоту встречаемости тех аллелей, которые этот генотип составляют, и последующего суммирования значений все трех генотипов.
Таблица 8.1 Определение среднего значения генотипа в популяции
| Генотип | Частота | Значение | Частота X значение |
| АА | Р2 | +d | p2d |
| Аа Аа | 2pq q2 | h -d | 2pqh -q2d |
| I = d(p2— q2)+2hpq |
Значение М=d(p2 — q2) + 2hpq представляет собой одновременно и фенотипическое и генотипическое значения среднего в популяции при допущении, что средовая дисперсия в популяции равна 0. Таким образом, вклад любого локуса в популяционное среднее определяется двумя величинами: величиной d(р2 - q), приписываемой влиянию гомозиготности, и 2hpq, приписываемой влиянию гетерозиготности. При отсутствии доминантности (h = 0) значение второго термина равно 0 и, соответственно, популяционное среднее пропорционально генной частоте М = d(1 — 2q). В случае полной доминантности (h = d) популяционное среднее пропорционально квадрату генной частоты М = d(1 — 2q ). При отсутствии сверхдоминантности разброс значений, приписываемых локусу, равняется 2d (иначе говоря, если аллель А фиксирован в популяции, т.е. р = 1, то популяционное среднее будет равно d; если же в популяции фиксирован аллель а, т.е. q = 1, популяционное среднее будет равно -d). Однако при сверхдоминантности локуса среднее в популяции с отсутствием фиксации может лежать за пределами этого спектра.
ПОЛИГЕННЫЕ ГЕНЕТИЧЕСКИЕ МОДЕЛИ
Одним из центральных допущений генетики количественных признаков, в том числе и психологических, является допущение о возможности суммирования генетических эффектов каждого локуса внутри
генетической системы, включающей несколько локусов. Иными словами, если генетическая система состоит из двух локусов, А и В, то при определении генетического эффекта всей системы генетические эффекты А (аддитивные и доминантные) суммируются с генетическими эффектами В (аддитивными и доминантными). Кроме того, при характеристике общего генетического эффекта этой системы необходимо учитывать эффекты, возникающие в результате взаимодействия между локусами А и В. Эти эффекты называются эпистатическими эффектами.
Эпистатические эффекты. Напомним, что доминантность возникает в результате неаддитивных взаимодействий аллелей в одном ло-кусе. Подобным же образом аллели разных локусов, функционируя в рамках одной генетической системы, могут взаимодействовать, приводя к возникновению так называемого эпистаза. Таким образом, в отличие от доминантности, возникающей в результате взаимодействия аллелей внутри одного локуса, эпистаз есть результат взаимодействия аллелей разных локусов.
Итак, генетические эффекты, возникающие в рамках полигенной модели, бывают трех типов: аддитивные (А), доминантные (D) и эпистатические (I). Представим это заключение символически:
G = А + D + I.
Соответственно сказанному выше, G представляет собой сумму всех генетических влияний в рамках полигенной системы; А — сумму всех аддитивных влияний для всех локусов, входящих в данную систему; D отражает все доминантные влияния в данной системе, и I характеризует генетические влияния, которые возникают в результате взаимодействия аллелей разных локусов, включенных в данную систему.
Фенотипическое значение. Мы рассмотрели представления генетики количественных признаков о генетических влияниях на формирование межиндивидуальной вариативности непрерывно распределенных признаков. Однако совершенно очевидно, что на поведенческие признаки оказывает влияние и среда. Количественная генетическая модель предполагает, что межиндивидуальная вариативность по признаку в популяции определяется как генетическими, так и средовыми факторами. Иными словами,
Р=G+Е+ (GxЕ),
где Р — наблюдаемые (фенотипические) значения признака в некоторой популяции. Р — функция генетических (G) и средовых (Е) отклонений от, соответственно, генотипического и средового средних, и некоего интеракционистского члена GxE, который отражает влияния, возникающие в результате взаимодействия генотипа и среды (ГС-взаимодействия и ГС-корреляции).
Как уже было сказано (гл. V), популяцией называется группа индивидов, проживающих на определенной территории, имеющих общий язык, общую историю и культуру и характерный генофонд, сформированный и сохранившийся в результате того, что члены популяции вступают в браки между собой намного чаще, чем с представителями других популяций. Члены популяции похожи друг на друга (или отличаются друг от друга) по набору морфологических, физиологических, психологических и других характеристик, называемых в генетике признаками. Напомним, что измеряемое значение любого признака называется фенотипом (гл. I), он является результатом реализации данного генотипа в данной среде. Популяционный разброс по изучаемому признаку (популяционная вариативность признака) называется фенотипической дисперсией (Vp) и вычисляется по формуле:
(X1 -X)2
N-l
где N— количество индивидов в исследуемой популяции, Хi— значение исследуемого признака у i-го члена популяции (т.е. его фенотип), аX— популяционное среднее по исследуемому признаку.
Теперь запишем обе полученные формулы (для G и для Р) в терминах дисперсии:
VG = Cov(G)(G) = Cov(A + D + I) = VA+VD+VI+ 2Cov(A)(I) + 2Cov(D)(I) + 2Cov(A)(D).
При допущении независимости (т.е. отсутствия корреляции между
ними) A, D и /, члены уравнения, отражающие ковариации между
этими составляющими генотипической дисперсии, могут быть сокращены, Тогда
VG=VA+VD+Vj.
Иными словами, наблюдаемая генотипическая вариативность в популяции есть результат суммирования вариативности аддитивной, доминантной и эпистатической.
Подобным же образом в терминах дисперсии может быть записано фенотипическое разнообразие людей в популяции:
Vp = Cov(P)(P) = Cov[G + E + (GxE)][G + E + (GxE)] =
= VG+VE+2Cov(G)(E) + VGxE.
Иначе говоря, количественные психогенетические модели основаны на допущении, что популяционная фенотипическая вариативность может быть объяснена влиянием генетических (VG) и средовых факторов (VE ), а также гено-средовых эффектов, возникающих в результате соприсутствия этих двух факторов [генотип-средовой ковариации
Cov(G)(E) и генотип-средового взаимодействия (VGxe)]. Если всю фе-нотипическую изменчивость принять за 100%, то вклады генотипа, среды и генотип-средовых эффектов тоже могут быть выражены в процентах. Иными словами, когда говорят, что вклад генотипа в формирование межиндивидуальной вариативности признака составляет 60%, это означает, что на все остальные составляющие приходится 40%, Распределение фенотипических значений признака в популяции может быть представлено в качестве суммы разбросов определенных значений (см. табл. 8.2).
Таблица 8.2 Структура фенотипической вариативности признака впопуляции
| Составляющая изменчивости | Символ | Значение, для которого |
| определяется дисперсия | ||
| Фенотипическая | V, | Фенотипическое значение |
| Генотипическая | Генотипическое значение | |
| Аддитивная | VA | Аддитивное значение |
| Доминантная | VD | Доминантность |
| Эпистатическая | У> | Значение эффекта |
| взаимодействия генов | ||
| Средовая | VE | Средовые отклонения |
В обобщенном виде задачу генетики количественных признаков можно сформулировать так; установление того, какие компоненты и в какой степени определяют вариативность фенотипических значений исследуемого признака.
Рассмотрим далее составляющие психогенетической количественной модели подробнее.
ГЕНЕТИЧЕСКИЕ ЭФФЕКТЫ
Изучая механизм генетического контроля того или иного признака, исследователи ставят перед собой задачу найти ответы на четыре ключевых вопроса: 1) Насколько сильно влияние генотипа на формирование различий между людьми? 2) Каков биологический механизм этого влияния (сколько и какие гены вовлечены, каковы их функции и где, на каком участке какой хромосомы, они локализованы? 3) Каковы биологические процессы, соединяющие белковый продукт генов и конкретный фенотип? 4) Существуют ли какие-нибудь средовые факторы, влияние которых может привести к изменению исследуемого генетического механизма, и если существуют, то како-
ва величина их влияния? Остановимся несколько подробнее на первом вопросе, хотя современная психогенетика занимается поисками ответов на все указанные вопросы.
Итак, описываемая модель, адресующаяся к первому из названных вопросов, не отвечает на вопрос «как?», ее цель — выяснить, насколько сильно влияние генотипа на формирование индивидуальных различий. Влияние генотипа выражается относительной величиной, отражающей размерность вклада генов в фенотипическую дисперсию. Этой величиной является коэффициент наследуемости, вычисляемый как отношение вариативности генетической к вариативности фенотипической:
h2=VG/VP.
Экспериментальные генетические исследования, проведенные с растениями и животными, показали, что коэффициент наследуемости является суммарной величиной и включает как аддитивные, так и неаддитивные, возникающие в результате взаимодействия, генетические эффекты.
Выделяют два типа коэффициента наследуемости: один из них оценивает наследуемость в широком смысле, второй — в узком. Первый (его иногда называют также коэффициентом генетической детерминации) говорит о том, насколько популяционная изменчивость фенотипического признака определяется генетическими различиями между людьми. Его величина может варьировать от 0 до 1, т.е. теоретически изменчивость признака может и совсем не зависеть от вариативности генотипов и, наоборот, полностью определяться ею; чем выше значение этого коэффициента, тем выше роль наследственности в формировании индивидуальных различий.
Второй коэффициент оценивает только ту долю изменчивости, которая связана с аддитивным действием генов; благодаря этому он позволяет получить сведения не о причинах популяционной изменчивости признака, а о свойствах гамет и генов, полученных потомками от своих родителей. Вот почему, например, в селекции животных и растений именно он используется при селекционировании.
Для обозначения рассматриваемых коэффициентов разные авторы используют разные символы. Мы примем те, которые предложены в авторитетном руководстве «Генетика человека», написанным Ф. Фогелем и А. Мотульски [159]. Авторы определяют наследуемость в широком смысле формулой:
h2=VG/VP,
где VG— общая генотипическая дисперсия, включающая доминирование, эпистаз и аддитивные составляющие.
Наследуемость в узком смысле определяется формулой:
h2=VA/VP, 192
Таким образом, эти коэффициенты различаются только числителями дроби: если в числителе находится суммарная генотипическая вариативность в популяции (VG ) — речь идет о наследуемости в широком смысле; если же в числителе VA , то имеется в виду наследуемость в узком смысле.
Как и любой статистический показатель, коэффициент наследуемости предполагает определенные допущения и ограничения, поэтому интерпретироваться должен грамотно. Фогель и Мотульски выделяют три свойства коэффициента наследуемости.
1. Поскольку коэффициент наследуемости есть отношение, его величина может изменяться при изменении числителя (т.е. вариативности генотипов) или знаменателя (т.е. вариативности средовых условий). Он увеличивается, когда повышается генетическая дисперсия или, наоборот, снижается вариативность сред.
2. Оценка дисперсии основана на анализе корреляций между родственниками; этот анализ проводится по определенным правилам (см. далее), но они справедливы только при допущении случайного подбора супружеских пар. Применительно к психологии человека это допущение неверно, поэтому необходимы статистические поправки на ассортативность, в противном случае возникают систематические смещения в оценке h2.
3. Одно из главных допущений при вычислениях h2 — отсутствие ковари-ации и взаимодействия между генетическим значением и средовым отклонением, что также не всегда верно.
Все это необходимо иметь в виду при вычислении и, главное, интерпретации оценок наследуемости.
Кроме того, разные методы психогенетики имеют разную разрешающую способность оценки как h2, так и составляющих Vp. Например, метод близнецов не позволяет оценить VD , т.е. дисперсию доминирования. Он дает только суммарную оценку VD + VA. Правда, Фогель и Мотульски, опираясь на работу Д. Фальконера, считают, что составляющая VD обычно незначима по сравнению с VA, и поэтому допустимо предположение о том, что практически вся генотипическая вариативность сводится к аддитивной вариативности: VG = VA. Тогда формула коэффициента наследуемости примет вид h2 = VG / VP . Это GсильAно упрощает логику дальнейших рассуждений.
Анализу средовых и генотип-средовых эффектов была посвящена гл. VI. Обобщенная характеристика этих компонентов уравнения фе-нотипической дисперсии приведена в табл. 8.3.
Таблица 8.3 Компоненты фенотипической дисперсии
| Эффект | Обозначение | Тип эффекта |
| Общий средовой | VEC(или Vc) | средовой |
| Уникальный средовой | VEN(илиVN) | средовой |
| Генотип-средовая корреляция | СоrGE (или | генотип-средовой |
| Cor(G)(E)) | ||
| Генотип-средовое взаимо- | GхЕ(или VGxe) | генотип-средовой |
| действие | ||
| Ассортативность | Ц | генотип-средовой |
13- 1432
2. МЕТОДЫ АНАЛИЗА ПСИХОГЕНЕТИЧЕСКИХ ЭМПИРИЧЕСКИХ ДАННЫХ
Как говорилось в гл. VII, психогенетиками была разработана система методов, которые позволяют оценить составляющие фенотипи-ческой дисперсии; все они построены на решении систем уравнений, описывающих сходство родственников различных степеней родства. К их анализу мы теперь и переходим.
Дата добавления: 2015-07-18; просмотров: 926;
