Интерференция

При сложении двух гармонических колебаний у₁= a₁sin(ωt + φ₁) и у₂= a₂sin(ωt + φ₂) результирующее колебание также будет гармоническим

y = у₁ + у₂= Asin(ωt + θ),

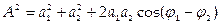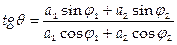где и . Квадрат амплитуды колебания определяет его энергию и, следовательно, энергия результирующего колебания зависит от разности фаз и может принимать любые значения в пределах от 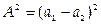при φ₁ — φ₂ = p до А² = (a₁ + а₂)² при φ₁– φ₂= 0.

Средняя интенсивность I за конечное время наблюдения τ равна

.

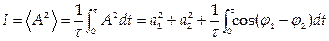При беспорядочном изменении фаз последний интеграл стремится к нулю и тогда I = I₁ + I₂.

При сложении колебаний различаются два случая:

1. Разность фаз сохраняется неизменной за время τ, достаточное для наблюдений. В этом случае колебания называются когерентными. Интенсивность результирующего колебания не равна сумме интенсивностей слагаемых и зависит от разности фаз.

2. Разность фаз беспорядочно меняется за время наблюдения. Такие колебания называются некогерентными. В этом случае интенсивность результирующего колебания равна сумме интенсивностей слагаемых.

Монохроматические волны одинаковой частоты всегда когерентны и поэтому могут интерферировать. Результат интерференции определяется разностью фаз в месте наблюдения. Эта разность зависит от начальной разности фаз φ иот разности расстояний d₂– d₁, отделяющих точку наблюдения от источников каждой из волн. Если амплитуды каждой из волн одинаковы и равны а, то интенсивность результирующей волны дается выражением: 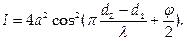Если начальные фазы одинаковы (φ = 0), то при d₂– d₁ = mλ/2, где m — четное число, интенсивность достигает максимума. При нечетном m интенсивность минимальна (в нашем случае — нуль).

Обычные (нелазерные) источники света некогерентны. Поэтому для наблюдения интерференции используются специальные приспособления, расщепляющие свет от одного источника на два пучка и затем сводящие их в некоторой области пространства вместе (например, бизеркала Френеля, билинзы Билле и др.) Интерференцией объясняются цвета тонких пленок, кольца Ньютона и другие явления.