Ток смещения. Электромагнитное поле
Явление электромагнитной индукции устанавливает связь между изменяющимся во времени магнитным полем и вихревым электрическим полем. Максвелл предположил существование и обратной связи, т. е. изменяющееся во времени электрическое поле должно приводить к появлению магнитного поля. Для установления соотношений между переменным электрическим и возникающим магнитным полями Максвелл ввел в рассмотрение так называемый ток смещения.
Пусть плоский конденсатор, площадь пластин которого S, заряжен с поверхностной плотностью заряда 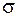 (рис. 98.1). Рассмотрим процессы, протекающие при зарядке и разрядке конденсатора во внешней цепи и в пространстве между его пластинами. В соединяющем обкладки проводнике и в самих пластинах конденсатора возникает ток проводимости
(рис. 98.1). Рассмотрим процессы, протекающие при зарядке и разрядке конденсатора во внешней цепи и в пространстве между его пластинами. В соединяющем обкладки проводнике и в самих пластинах конденсатора возникает ток проводимости 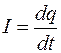 .
.
Так как заряд конденсатора равен 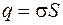 , то
, то  . Тогда для плотности тока проводимости имеем
. Тогда для плотности тока проводимости имеем
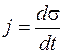 . (98.1)
. (98.1)
Направление линий вектора 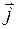 во внешней цепи – от положительно заряженной пластины конденсатора к отрицательной. Движение свободных носителей заряда, т. е. ток проводимости, имеет место во всей цепи, кроме пространства между обкладками конденсатора. Следовательно, линии тока проводимости терпят на границах пластин разрыв.
во внешней цепи – от положительно заряженной пластины конденсатора к отрицательной. Движение свободных носителей заряда, т. е. ток проводимости, имеет место во всей цепи, кроме пространства между обкладками конденсатора. Следовательно, линии тока проводимости терпят на границах пластин разрыв.
В пространстве между обкладками конденсатора существует переменное электрическое поле, для которого в любой момент времени электрическая индукция согласно формуле (47.2) равна поверхностной плотности заряда: 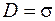 . Так как при разрядке конденсатора s изменяется, то можно найти
. Так как при разрядке конденсатора s изменяется, то можно найти
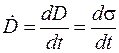 . (98.2)
. (98.2)
При зарядке конденсатора на левой обкладке будет накапливаться положительный заряд (рис. 98.1, а). В этом случае ток 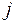 в проводнике течет от правой пластины к левой, заряд конденсатора увеличивается, поэтому
в проводнике течет от правой пластины к левой, заряд конденсатора увеличивается, поэтому 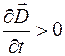 ; векторы электрической индукции
; векторы электрической индукции 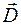 и скорости ее изменения
и скорости ее изменения 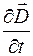 совпадают по направлению. Из рисунка видно, что направление векторов
совпадают по направлению. Из рисунка видно, что направление векторов 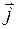 и
и 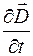 также совпадают. А это означает, что линии
также совпадают. А это означает, что линии  в пространстве между обкладками конденсатора продолжают линии
в пространстве между обкладками конденсатора продолжают линии 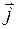 в проводнике. Кроме того, из формул (98.1) и (98.2) следует, что густота линий
в проводнике. Кроме того, из формул (98.1) и (98.2) следует, что густота линий 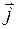 и линий
и линий  совпадает. Максвелл назвал величину
совпадает. Максвелл назвал величину 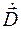 плотностью тока смещения, т. е.
плотностью тока смещения, т. е.
 |
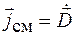 . (98.3)
. (98.3)
При разрядке конденсатора (рис. 98.1, б) ток течет от левой обкладки к правой, поле конденсатора ослабляется, поэтому 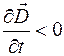 . Направления векторов
. Направления векторов 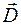 и
и 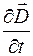 оказываются противоположными, однако векторы
оказываются противоположными, однако векторы 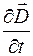 и
и 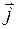 опять сонаправлены. А это снова означает, что линии векторов
опять сонаправлены. А это снова означает, что линии векторов 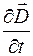 и
и 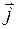 продолжают друг друга.
продолжают друг друга.
Изменение вектора электрической индукции 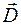 согласно формуле (47.6) может быть обусловлено как изменением напряженности электрического поля
согласно формуле (47.6) может быть обусловлено как изменением напряженности электрического поля 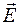 , так и изменением поляризованности
, так и изменением поляризованности 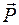 . В соответствии с этим плотность тока смещения может определяться по формуле
. В соответствии с этим плотность тока смещения может определяться по формуле
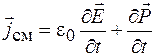
или
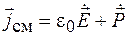 .
.
Второе слагаемое в этой формуле ( 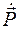 ) представляет собой плотность тока поляризации и учитывается только в диэлектриках. Первое слагаемое (
) представляет собой плотность тока поляризации и учитывается только в диэлектриках. Первое слагаемое ( 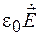 ) определяет плотность тока смещения в вакууме.
) определяет плотность тока смещения в вакууме.
Таким образом, по предположению Дж. К. Максвелла, линии тока проводимости в пространстве между обкладками конденсатора переходят в линии тока смещения. Однако следует помнить, что ток смещения есть лишь меняющееся во времени электрическое поле. Формулу (98.3), определяющую плотность тока смещения, Максвелл распространил на электрические поля любого вида, в том числе и на вихревые. Из всех физических свойств, присущих току проводимости, Максвелл приписал току смещения лишь одно – способность создавать в окружающем пространстве магнитное поле. Следовательно, всюду, где есть ток смещения, т. е. меняющееся во времени электрическое поле, возникает магнитное поле, в общем случае тоже переменное.
Если в какой-либо области пространства существует и ток проводимости, и ток смещения, то плотность полного тока
 . (98.4)
. (98.4)
Учитывая соотношение (98.3), формулу (98.4) запишем в виде
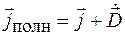 . (98.5)
. (98.5)
Согласно Дж. К. Максвеллу при расчетах магнитных полей во все формулы нужно подставлять полную плотность тока, определяемую равенством (98.5). Например, циркуляция вектора 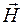 должна определяться выражением
должна определяться выражением
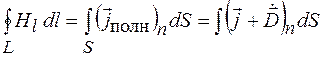
или
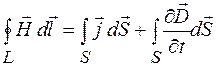 , (98.6)
, (98.6)
где j – плотность тока проводимости.
Уравнение (98.6) – наиболее важное в электромагнитной теории Максвелла.
Максвелл изменил существующие представления о замкнутости электрических цепей. В цепи с конденсатором постоянный ток протекать не может, для него она разомкнута. Однако переменный (изменяющийся) ток в такой цепи протекает. По Максвеллу, цепи любых непостоянных токов замкнуты. Замкнутость таких цепей обеспечивается токами смещения, которые существуют в тех местах, где нет проводников.
Согласно идеям Максвелла переменное магнитное поле всегда связано с порожденным им электрическим полем; в свою очередь, переменное электрическое поле всегда связано с порожденным им магнитным полем. Совокупность переменных электрического и магнитного полей образует единое электромагнитное поле. Для существования электромагнитного поля оба образующих его поля – электрическое и магнитное – должны быть обязательно переменными.
Графическое изображение электромагнитного поля показано на рисунке 98.2. Векторы напряженности электрического и магнитного полей взаимно перпендикулярны: 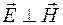 .
.
 Из принципа относительности вытекает, что раздельное рассмотрение электрического и магнитного полей имеет лишь относительный смысл. Электрическое поле создают неподвижные заряды. Однако если заряды неподвижны относительно некоторой инерциальной системы отсчета, то относительно других инерциальных систем эти заряды движутся и, следовательно, будут порождать не только электрическое, но и магнитное поле. Неподвижный проводник с током создает в каждой точке пространства магнитное поле. Но относительно других инерциальных систем этот проводник находится в движении. Поэтому создаваемое им магнитное поле в любой точке будет меняться и, следовательно, порождать вихревое электрическое поле. Таким образом, поле, которое относительно некоторой системы отсчета оказывается "чисто" электрическим или "чисто" магнитным, относительно других систем отсчета будет представлять собой совокупность электрического и магнитного полей, а если эти поля переменные, то они образуют единое электромагнитное поле.
Из принципа относительности вытекает, что раздельное рассмотрение электрического и магнитного полей имеет лишь относительный смысл. Электрическое поле создают неподвижные заряды. Однако если заряды неподвижны относительно некоторой инерциальной системы отсчета, то относительно других инерциальных систем эти заряды движутся и, следовательно, будут порождать не только электрическое, но и магнитное поле. Неподвижный проводник с током создает в каждой точке пространства магнитное поле. Но относительно других инерциальных систем этот проводник находится в движении. Поэтому создаваемое им магнитное поле в любой точке будет меняться и, следовательно, порождать вихревое электрическое поле. Таким образом, поле, которое относительно некоторой системы отсчета оказывается "чисто" электрическим или "чисто" магнитным, относительно других систем отсчета будет представлять собой совокупность электрического и магнитного полей, а если эти поля переменные, то они образуют единое электромагнитное поле.
Дата добавления: 2015-08-08; просмотров: 1298;
