Магнитные цепи. Магнитные цепи широко используются в современной электротехнике

Магнитные цепи широко используются в современной электротехнике. Действие электромагнитов, генераторов электрического тока, электродвигателей, трансформаторов и многих измерительных приборов основано на существовании в них магнитного потока. Для усиления магнитного потока почти всегда применяются ферромагнитные материалы. Изготавливая из этих материалов тела различной формы и размеров, оказывается возможным создавать магнитные потоки нужной величины в выбранном нами направлении. Совокупность тел, внутри которых проходят замкнутые линии магнитной 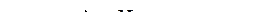индук-ции, называют магнитной цепью. Рассмотрим простую неразветвленную магнитную цепь (рис. 95.1). Эта цепь составлена из сердечника длиною l и воздушного зазора дли- ною 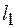. Магнитное поле создает обмотка с током 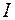, состоящая из N витков. По закону полного тока для напряженности магнитного по-ля (71.4)

, (95.1)

где Н, 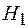– напряженность магнитного поля внутри сердечника и зазора соответственно.

Из соотношени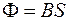й и 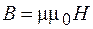находим:

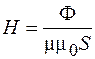, (95.2)

где S – сечение сердечника.

Так как линии вектора магнитной индукции непрерывны, то значения магнитного потока Ф внутри сердечника и внутри зазора одинаковы. Тогда, объединяя выражения (95.1) и (95.2), получаем:

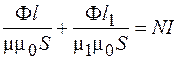, (95.3)

где 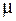– относительная магнитная проницаемость материала сердечника; – относительная магнитная проницаемость вещества зазора ( 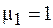для воздушного зазора).

Из соотношения (95.3) находим магнитный поток:

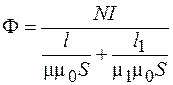. (95.4)

Формула (95.4) подобна закону Ома: .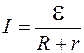

Из сравнения этих выражений получаем, что величина

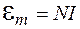(95.5)

играет роль ЭДС. Поэтому ее называют магнитодвижущей силой. Из формулы (95.5) следует, что единицей магнитодвижущей силы является ампер.

Из аналогии выражений закона Ома и (95.4) вытекает, что величина

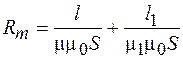(95.6)

входит в формулу так же, как и полное сопротивление цепи в закон Ома, и поэтому ее называют полным магнитным сопротивлением цепи.

Величины 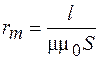и 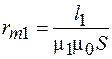называются магнитными сопротивлениями участков цепи. Магнитное сопротивление зависит от длины магнитопровода l и его сечения S так же, как и электрическое сопротивление, но роль удельной проводимости 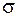играет величина . Объединяя выражения (95.4), (95.5) и (95.6), получаем:

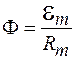, (95.7)

где

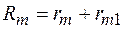. (95.8)

На основании формулы (95.7) заключаем, что магнитный поток равен отношению магнитодвижущей силы к полному магнитному сопротивлению цепи.

Из формулы (95.7) следует, что единица магнитного сопротивления – ампер на вебер (А/Вб). Формула (95.8) показывает, что полное магнитное сопротивление цепи равно сумме магнитных сопротивлений ее частей. Этот результат справедлив и в том случае, если цепь состоит из любого числа частей, если только магнитный поток проходит целиком через эти части: при последовательном соединении магнитопроводов их магнитные сопротивления складываются.

Следует отметить, что введенные термины и понятия (магнитодвижущая сила и магнитное сопротивление) имеют лишь формальный характер. Наряду с простой магнитной цепью на практике приходится встречаться с более сложными цепями, в которых происходит разветвление магнитного потока. В этом случае удобно использовать правила Кирхгофа, которые для магнитной цепи имеют вид

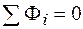, (95.9)

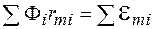. (95.10)

Пользуясь этими правилами, можно рассчитать любую разветвленную магнитную цепь.