Допускающие понижение степени.

Уравнение вида

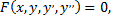
где 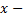независимая переменная, 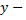искомая функция, ее производные, называется дифференциальным уравнением второго порядка.

Уравнения, разрешенные относительно второй производной в общем виде можно записать

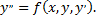
Так же как и для дифференциального уравнения первого порядка, решением уравнения

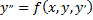
называется функция 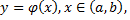которая при подстановке в уравнение обращает его в тождество.

Для уравнения второго порядка имеет место теорема существования и единственности решения – теорема Коши.

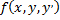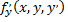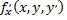Если функция и ее частные производные и определены и непрерывны в некоторой области 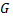пространства переменных 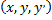, то какова бы ни была внутренняя точка 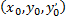области 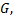в некоторой окрестности точки существует единственное решение уравнения

удовлетворяющее условиям

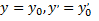при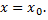

Геометрически это означает, что через заданную точку 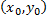плоскости проходит единственная интегральная кривая с заданным угловым коэффициентом касательной в этой точке.

Задачу отыскания решения по заданным начальным условиям называют задачей Коши.

Функция 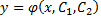называется общим решением уравнения 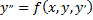в некоторой области 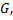если она является решением данного уравнения при любых значениях постоянных и и если при любых начальных условиях 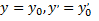при существуют единственные значения постоянных 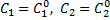такие, что функция удовлетворяет данным начальным условиям.

Любая функция получающаяся из общего решения 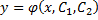уравнения 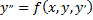при определенных значениях постоянных 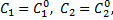называется частным решением.

Рассмотрим пример. Найти решение дифференциального уравнения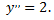

Общее решение данного уравнения найдем двукратным последовательным интегрированием. Последовательно интегрируя, находим сначала первую производную

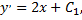
а затем и общее решение

.

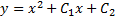Рассмотрим те случаи, когда решение уравнения

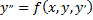
с помощью замены переменной сводится к решению уравнения первого порядка. Такое преобразование называется понижением порядка.

Уравнение вида

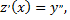Уравнение не содержит и Введем новую функцию полагая Тогда и уравнение превращается в уравнение первого порядка 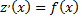с искомой функцией 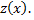Решая его, находим

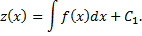
Так как 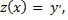то

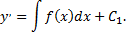
Отсюда, интегрируя еще раз, получаем искомое решение

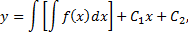
где и 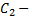произвольные постоянные.

Рассмотрим пример. Найти общее решение уравнения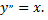

Полагая получаем уравнение первого порядка 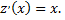Интегрируя его, найдем

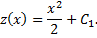
Заменяя 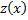на 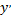и интегрируя еще раз, находим искомое общее решение

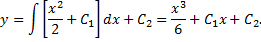
Уравнение вида

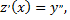Уравнение не содержит Положим тогда и уравнение преобразуется в уравнение первого порядка относительно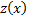

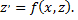
Решая его, найдем

Так как 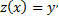, то Отсюда, интегрируя еще раз, получаем искомое решение

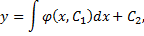
где и 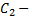произвольные постоянные.

Рассмотрим пример. Найти общее решение уравнения

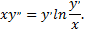
Понизим порядок этого уравнения, пусть 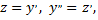получим однородное дифференциальное уравнение первого порядка относительно искомой функции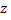

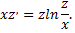
Решаем его с помощью подстановки 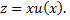Тогда

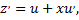
и уравнение принимает вид

Разделяя переменные и интегрируя, последовательно находим

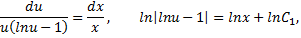
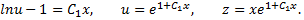
Так как то последнее уравнение является дифференциальным уравнением первого порядка, которое решается однократным интегрированием

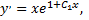
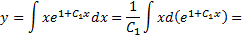
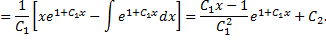
Получили общее решение исходного дифференциального уравнения.

Рассмотрим пример. Найти общее решение уравнения

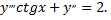
Вводим новую функцию 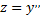и получаем из исходного уравнения линейное уравнение

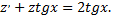
Сделаем замену

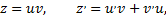
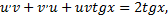
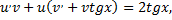
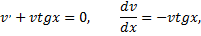
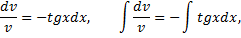
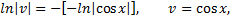
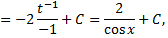
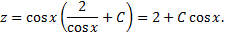
Так как 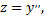то приходим к дифференциальному уравнению

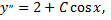
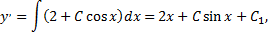
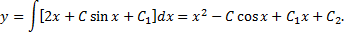
Линейные дифференциальные уравнения второго порядка в теории дифференциальных уравнений занимают важное место не только потому, что представляют собой простой и хорошо изученный тип уравнений, но и потому, что многие практические задачи физики, техники и особенно электротехники приводят к решению этих уравнений.