Дифференциальные уравнения первого порядка. Теорема Коши. Понятие об общем и частном решении дифференциального уравнения. Дифференциальные уравнения с разделяющими переменными.
Дифференциальные уравнения первого порядка.
Общий вид дифференциальных уравнений первого порядка
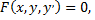
где 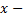 независимая переменная,
независимая переменная, 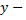 искомая функция,
искомая функция, 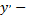 производная этой искомой функции.
производная этой искомой функции.
Если дифференциальное уравнение можно разрешить относительно 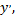 то оно примет вид
то оно примет вид
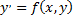
и называется уравнением первого порядка, разрешенным относительно производной.
Уравнение
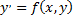
можно записать в виде
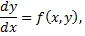
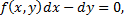
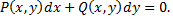
Решением дифференциального уравнения первого порядка называется функция 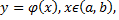 которая, при подстановке в уравнение, обращает его в тождество.
которая, при подстановке в уравнение, обращает его в тождество.
Рассмотрим пример. Функция 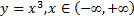 является решением уравнения
является решением уравнения 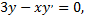 т.е.
т.е.

При каких условиях уравнение 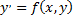 имеет решение, дает теорема Коши: если функция
имеет решение, дает теорема Коши: если функция  и ее частная производная
и ее частная производная 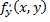 определены и непрерывны в некоторой области
определены и непрерывны в некоторой области 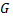 плоскости
плоскости  то какова бы ни была внутренняя точка
то какова бы ни была внутренняя точка 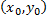 области
области 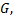 в некоторой окрестности этой точки существует единственное решение уравнения
в некоторой окрестности этой точки существует единственное решение уравнения 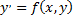 , удовлетворяющее условиям
, удовлетворяющее условиям 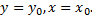
Теорема Коши дает возможность по виду дифференциального уравнения 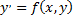 решать вопрос о существовании и единственности его решения. Это особенно важно в тех случаях, когда заранее неизвестно, имеет ли данное уравнение решение.
решать вопрос о существовании и единственности его решения. Это особенно важно в тех случаях, когда заранее неизвестно, имеет ли данное уравнение решение.
Геометрически теорема утверждает, что через каждую внутреннюю точку 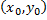 области
области 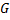 проходит единственная интегральная кривая.
проходит единственная интегральная кривая.
Отыскание решения уравнения 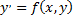 , удовлетворяющего начальным условиям, - одна из важнейших задач теории дифференциальных уравнений. Эта задача называется задачей Коши. С геометрической точки зрения решить задачу Коши – значит, из множества интегральных кривых выделить ту, которая проходит через заданную точку
, удовлетворяющего начальным условиям, - одна из важнейших задач теории дифференциальных уравнений. Эта задача называется задачей Коши. С геометрической точки зрения решить задачу Коши – значит, из множества интегральных кривых выделить ту, которая проходит через заданную точку 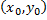 плоскости
плоскости 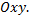
Общим решением дифференциального уравнения 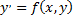 в области
в области 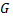 плоскости
плоскости 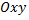 называется функция
называется функция  зависящая от
зависящая от  и произвольной постоянной
и произвольной постоянной 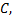 если она является решением уравнения
если она является решением уравнения 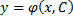 при любом значении постоянной
при любом значении постоянной 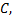 и если при любых начальных условиях
и если при любых начальных условиях 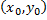 таких, что
таких, что 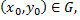 существует единственное значение постоянной
существует единственное значение постоянной 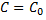 такое, что функция
такое, что функция 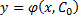 удовлетворяет данным начальным условиям
удовлетворяет данным начальным условиям 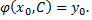
Частным решением дифференциального уравнения 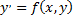 в области
в области 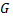 называется функция
называется функция 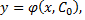 которая получается из общего решения
которая получается из общего решения 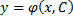 при определенном значении постоянной
при определенном значении постоянной 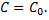
Решение или интеграл, полученные из общего решения или общего интеграла при фиксированных значениях произвольных постоянных 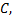 называется соответственно частным решением или частным интегралом дифференциального уравнения.
называется соответственно частным решением или частным интегралом дифференциального уравнения.
Рассмотрим пример. Уравнение первого порядка 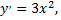 которое удовлетворяет всем условиям теоремы Коши, так как
которое удовлетворяет всем условиям теоремы Коши, так как 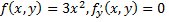 определены и непрерывны на всей области
определены и непрерывны на всей области 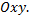 Общее решение уравнения
Общее решение уравнения 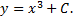 Если заданы начальные условия, то можно решить задачу Коши. Если
Если заданы начальные условия, то можно решить задачу Коши. Если 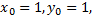 то
то 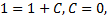 тогда частное решение
тогда частное решение 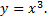
Рассмотрим пример:
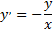
Функция

непрерывны при 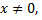 следовательно, во всей области
следовательно, во всей области  кроме оси
кроме оси 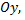 это уравнение удовлетворяет условиям Коши.
это уравнение удовлетворяет условиям Коши.
Дифференциальные уравнения с разделяющимися переменными.
Уравнение вида
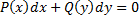
называется дифференциальным уравнением с разделенными переменными. Его общим интегралом будет интеграл
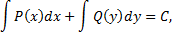
где 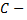 произвольная постоянная.
произвольная постоянная.
Уравнение вида
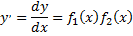
также уравнения, которые, с помощью алгебраических преобразований, приводятся к уравнениям с разделяющимся переменными. Разделение переменных выполняется следующим образом. Обе части уравнения
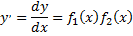
умножим на 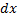 и, разделим на
и, разделим на 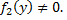 В результате получим уравнения с разделенными переменными
В результате получим уравнения с разделенными переменными

Рассмотрим пример. Найти общее решение дифференциального уравнения
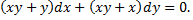
Предположим, что 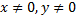 и разделим обе части данного уравнения на
и разделим обе части данного уравнения на 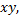 получим уравнение с разделенными переменными
получим уравнение с разделенными переменными
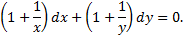
Интегрируем данное уравнение, последовательно получим
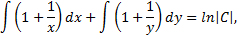
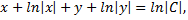
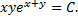
Последнее равенство является общим интегралом исходного дифференциального уравнения. При его нахождении были приняты ограничения 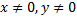 . Однако функции
. Однако функции  является решениями исходного дифференциального уравнения, они получаются при
является решениями исходного дифференциального уравнения, они получаются при 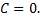 Таким образом,
Таким образом,  – частные решения исходного уравнения.
– частные решения исходного уравнения.
Рассмотрим пример. Найти частное решение уравнения
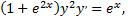
удовлетворяющее начальному условию 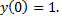
Запишем данное уравнение в дифференциальной форме
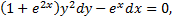
разделим переменные

Проинтегрируем последнее уравнение


Получили общее решение исходного уравнения. Использовав начальное условие, определим значение произвольной постоянной

Частное решение исходного дифференциального уравнения имеет вид
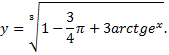
Контрольные вопросы
1. Сформулировать задачи, приводящие к составлению и решению дифференциальных уравнений.
2. Записать общий вид дифференциальных уравнений с разделяющими переменными.
3. Дать определение общего и частного решения дифференциального уравнения.
Дата добавления: 2015-08-11; просмотров: 1746;
