Различные формы записи комплексного числа. Формула Эйлера. Алгебраические действия над комплексными числами

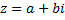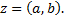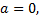Форма записи комплексного числа называется алгебраической формой комплексного числа Если то число 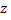называется мнимым, если 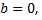то число 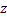будет действительным.

Два комплексных числа отличающиеся только знаками мнимой части, называются комплексно сопряженными числами.

Комплексное число 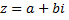равно нулю тогда, и только тогда, когда его действительная и мнимая части равны нулю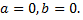

Алгебраическая форма записи существенно облегчает выполнение арифметических операций над комплексными числами, как над обычными двучленами, учитывая, что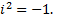

Пусть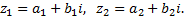

Сложение чисел 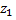и :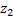

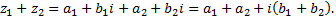
Вычитание комплексных чисел 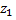и :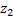

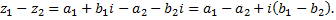
Умножение комплексных чисел 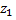и :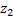

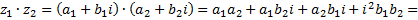
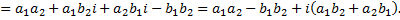
Произведение сопряженных комплексных чисел равно сумме квадратов их действительной и мнимой частей

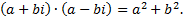
Деление комплексных чисел 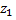и :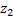

Рассмотрим пример. Представить комплексные числа в алгебраической форме и выполнить операции сложения, вычитания, умножения и деления

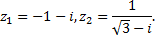
1)

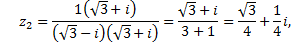
2)

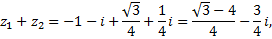
3)

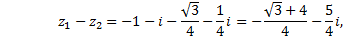
4)

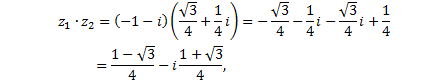
5)

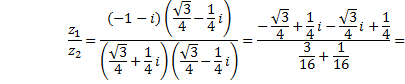
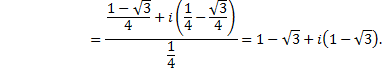
Показательная форма записи комплексного числа.

Пусть 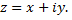Определим показательную функцию комплексного переменного

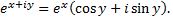
Положим 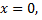получим формулу Эйлера, выражающую показательную функцию с мнимым показателем через тригонометрические функции

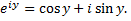
Напомним, что комплексное число в тригонометрической форме имеет вид

тогда, применив к записи комплексного числа в показательной форме, получим

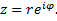
Арифметические действия над комплексными числами в показательной форме выполняются на основании свойств показательной функции.

Пусть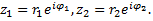

Произведение чисел 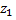и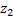

Частное чисел 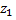и :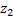

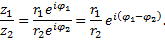
Возведение комплексного числа в степень:

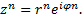
Извлечение корня n-й степени из комплексного числа :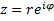

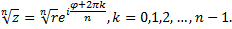
Контрольные вопросы

1. Какие числа называют комплексными?

2. Записать различные формы комплексного числа.

3. В каком случае применяют формулу Эйлера?

4. Перечислить алгебраические действия над комплексными числами.