Формула Грина
Связь между криволинейными и двойными интегралами устанавливает формула Грина.
Пусть  некоторая простая замкнутая область (область, граница которой пересекается с прямыми параллельными осям координат, не более, чем в двух точках), ограниченная контуром
некоторая простая замкнутая область (область, граница которой пересекается с прямыми параллельными осям координат, не более, чем в двух точках), ограниченная контуром 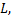 и пусть функции
и пусть функции 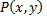 и
и 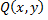 непрерывны вместе со своими частными производными
непрерывны вместе со своими частными производными 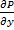 и
и  в данной области. Тогда имеет место формула
в данной области. Тогда имеет место формула
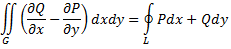
- это есть формула Грина.
Формула Грина остается справедливой для всякой замкнутой области 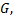 которую можно разбить проведением дополнительных линий на конечное число простых замкнутых областей.
которую можно разбить проведением дополнительных линий на конечное число простых замкнутых областей.
Рассмотрим пример. С помощью формулы Грина вычислить криволинейный интеграл
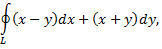
где 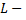 окружность
окружность 
Функции
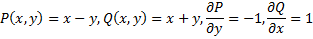
непрерывны в замкнутом круге 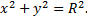
Следовательно, формула Грина применима к данному интегралу
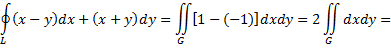
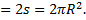
В некоторых случаях величина криволинейного интеграла
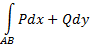
не зависит от интегрирования, а зависит от начальной и конечной точек  и
и 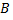 пути интегрирования. При каких условиях имеет место такая независимость?
пути интегрирования. При каких условиях имеет место такая независимость?
Плоская область 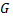 называется односвязной, если каков бы ни был замкнутый контур
называется односвязной, если каков бы ни был замкнутый контур 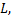 лежащий внутри этой области, ограниченная этим контуром часть плоскости целиком принадлежит области
лежащий внутри этой области, ограниченная этим контуром часть плоскости целиком принадлежит области 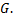 Односвязность области означает, что область не имеет дыр. Например, односвязными областями являются внутренность круга, эллипса, многоугольника и так далее.
Односвязность области означает, что область не имеет дыр. Например, односвязными областями являются внутренность круга, эллипса, многоугольника и так далее.
Пусть функции 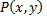 и
и 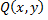 определены и непрерывны вместе со своими частными производными
определены и непрерывны вместе со своими частными производными 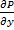 и
и  в некоторой замкнутой односвязной области
в некоторой замкнутой односвязной области 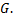 Тогда следующие условия эквивалентны, т.е. выполнение любого из них влечет за собой выполнение остальных трех:
Тогда следующие условия эквивалентны, т.е. выполнение любого из них влечет за собой выполнение остальных трех:
1) для любой замкнутой кусочно-гладкой кривой 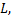 расположенной в области
расположенной в области 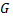
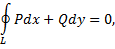
2) для любых двух точек 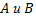 области
области 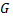 значение интеграла
значение интеграла
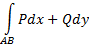
не зависит от выбора пути интегрирования, целиком лежащего в области 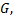
3) выражение 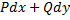 представляет собой полный дифференциал некоторой функции, определенной в области
представляет собой полный дифференциал некоторой функции, определенной в области 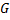
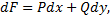
4) в области 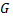 всюду
всюду
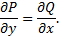
Контрольные вопросы
1. Дать определение криволинейного интеграла.
2. Как вычисляют криволинейные интегралы первого и второго рода?
3. Сформулировать условия независимости криволинейного интеграла от пути интегрирования.
4. Записать формулу Грина.
Дата добавления: 2015-08-11; просмотров: 1733;
