Вычисление криволинейных интегралов первого и второго рода. Условия независимости криволинейного интеграла от пути интегрирования
Вычисление криволинейных интегралов первого рода.
Пусть кривая 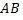 задана параметрическими уравнениями
задана параметрическими уравнениями
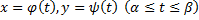
где 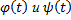 – непрерывные вместе со своими производными
– непрерывные вместе со своими производными 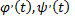 функции, а
функции, а 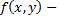 функция непрерывная вдоль этой кривой. Тогда для любой точки
функция непрерывная вдоль этой кривой. Тогда для любой точки 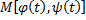 кривой
кривой 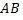 длину
длину 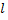 дуги
дуги 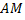 можно рассматривать как функцию параметра
можно рассматривать как функцию параметра 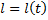 и вычислять по формуле
и вычислять по формуле

Откуда, согласно правилу дифференцирования интеграла по верхнему пределу,

Если кривая 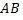 задана уравнением
задана уравнением 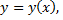 то
то
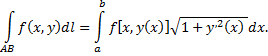
Рассмотрим пример. Вычислить криволинейный интеграл
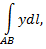
где 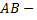 дуга параболы
дуга параболы 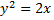 от точки
от точки 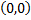 до точки
до точки 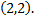
Воспользуемся формулой
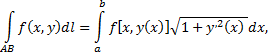
для этого определим
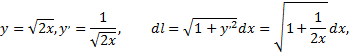
тогда

Вычисление криволинейных интегралов второго рода.
Криволинейные интегралы второго рода вычисляют сведением их к определенным интегралам.
Если кривая 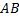 задана уравнением вида
задана уравнением вида
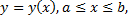
где 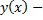 непрерывно дифференцируемая функция, то, принимая
непрерывно дифференцируемая функция, то, принимая  за параметр
за параметр
 получаем
получаем
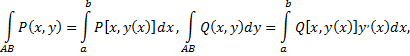
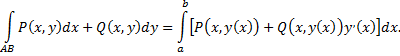
Аналогично поступаем, если кривая 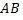 задана уравнением вида
задана уравнением вида 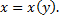
Рассмотрим пример. Вычислить интеграл
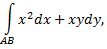
где 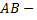 четверть окружности
четверть окружности
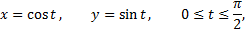
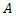 соответствует
соответствует 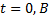 соответствует
соответствует 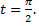
Имеем
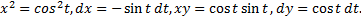
Получаем
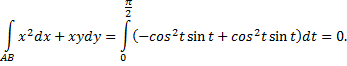
Рассмотрим пример. Вычислить интеграл
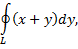
где 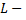 контур прямоугольника, образованного прямыми
контур прямоугольника, образованного прямыми 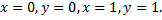
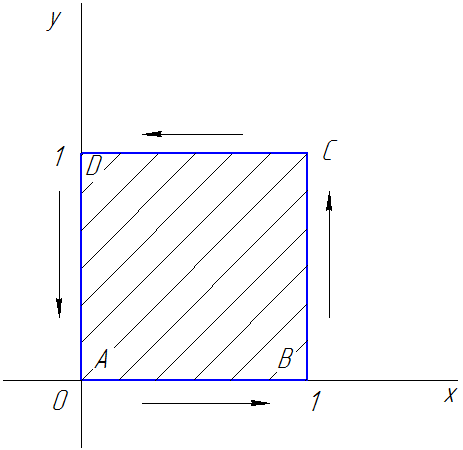
Рис. 61
Контур интегрирования
На рисунке 61 положительное направление обхода контура  обозначено стрелками. Разбивая весь контур интегрирования на части, получим
обозначено стрелками. Разбивая весь контур интегрирования на части, получим
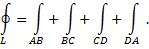
Интегралы вдоль участков 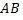 и
и 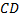 равны нулю, так как на них
равны нулю, так как на них  является постоянным и, следовательно,
является постоянным и, следовательно, 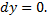 Остается вычислить интегралы по участкам
Остается вычислить интегралы по участкам 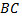 и
и 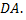
Получим
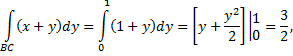

Окончательно получим
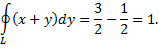
Дата добавления: 2015-08-11; просмотров: 3227;
