Геометрический смысл двойного интеграла
Вычисление площади посредством двойного интеграла.
Площадь 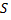 плоской области
плоской области 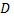 равна двойному интегралу от
равна двойному интегралу от 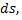 распространенному на область
распространенному на область 
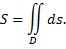
В прямоугольных координатах  и
и
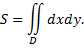
В полярных координатах 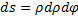 и
и
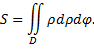
Рассмотрим пример. Найти площадь области, ограниченной линиями
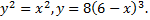
Построив данные полукубические параболы, получим криволинейный четырехугольник  Точки,
Точки,  и
и 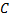 пересечения кривых найдены путем совместного решения их уравнений.
пересечения кривых найдены путем совместного решения их уравнений.
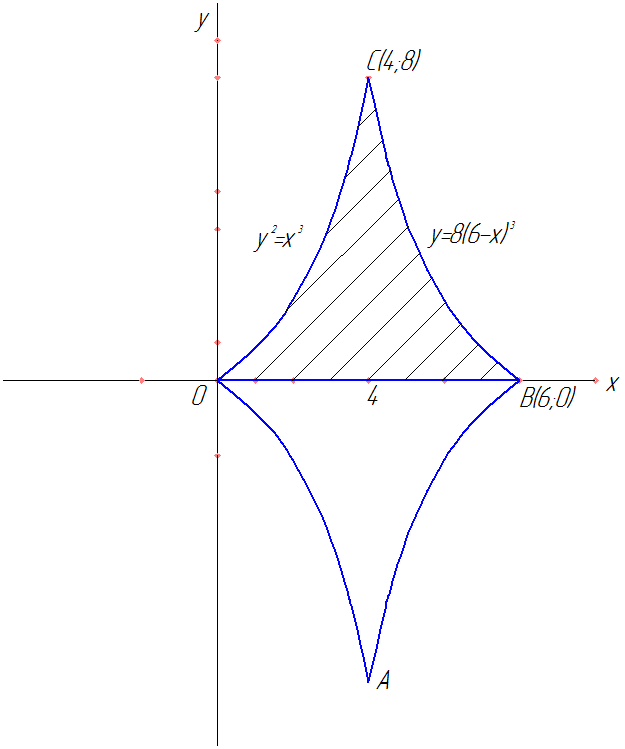
Рис. 55
Криволинейный четырехугольник
Вследствие симметричности фигуры относительно оси 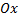 ее площадь
ее площадь 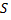 равна удвоенной площади криволинейного треугольника
равна удвоенной площади криволинейного треугольника 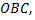 расположенного в первом квадрате.
расположенного в первом квадрате.
Согласно формуле
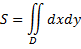
площадь области 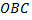 равна
равна
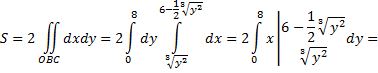
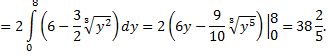
Если интегрировать в другом порядке, то необходимо разбить область 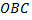 прямой, проходящей через точку
прямой, проходящей через точку 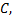 параллельно оси
параллельно оси 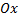 на две части
на две части
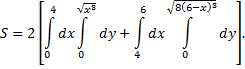
Результат при этом получится тот же самый.
Вычисление объема тела.
Объем вертикального цилиндрического тела, имеющего своим основанием область 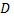 на плоскости
на плоскости 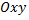 и ограниченного сверху поверхностью
и ограниченного сверху поверхностью 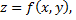 выражается двойным интегралом
выражается двойным интегралом
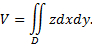
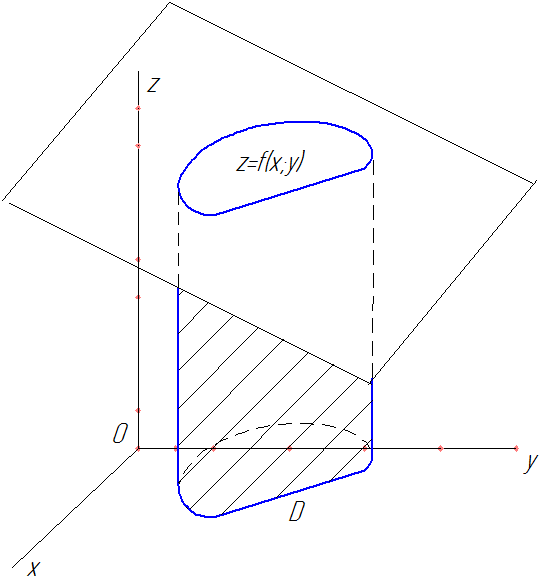
Рис. 56
Вертикальное цилиндрическое тело
Рассмотрим пример. Вычислить объем тела, ограниченного поверхностями
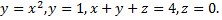
Данное тело представляет собой вертикальный цилиндр, который сверху ограничен плоскостью 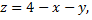 а снизу – частью плоскости
а снизу – частью плоскости  заключенной между параболой
заключенной между параболой
 и прямой
и прямой 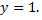
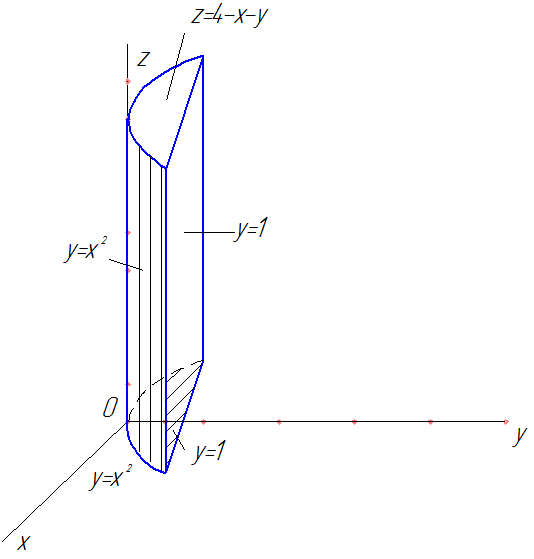
Рис. 57
Вертикальный цилиндр
Согласно формуле
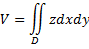
объем этого тела

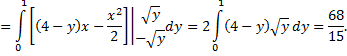
Дата добавления: 2015-08-11; просмотров: 1313;
