Сведение двойного интеграла к повторному. Изменение порядка интегрирования
Вычисление двойного интеграла
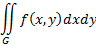
сводится к вычислению одного или нескольких двукратных интегралов

или
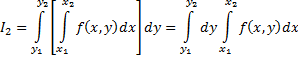
каждый, из которых есть результат последовательного вычисления двух обыкновенных определенных интегралов. Пределы при первом интегрировании являются переменными, зависят от той переменной, которая при этом рассматривается как постоянная. Пределы при втором интегрировании всегда постоянны.
Рассмотрим пример. Вычислить двойной интеграл

Сначала вычисляем внутренний интеграл, где  является переменной, а
является переменной, а  постоянной
постоянной

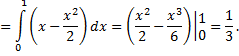
Правила вычисления двойных интегралов.
Различают два основных вида области интегрирования.
1)Область интегрирования  ограничена слева и справа прямыми
ограничена слева и справа прямыми 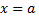 и
и  а снизу и сверху – непрерывными кривыми
а снизу и сверху – непрерывными кривыми 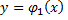 и
и  каждая из которых пересекается вертикальной прямой только в одной точке. Для такой области двойной интеграл вычисляется по формуле
каждая из которых пересекается вертикальной прямой только в одной точке. Для такой области двойной интеграл вычисляется по формуле


Рис. 48
Область, ограниченная прямыми
2)Область интегрирования 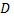 ограничена снизу и сверху прямыми
ограничена снизу и сверху прямыми  и
и  а слева и справа – непрерывными кривыми
а слева и справа – непрерывными кривыми 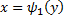 и
и 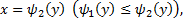 каждая из которых пересекается горизонтальной прямой только в одной точке. Для такой области двойной интеграл вычисляется по формуле
каждая из которых пересекается горизонтальной прямой только в одной точке. Для такой области двойной интеграл вычисляется по формуле


Рис. 49
Область, ограниченная прямыми
В более общем случае область интегрирования путем разбиения на части сводится к основным областям. Интеграл по исходной области заменяется равной ему суммой интегралов по ее частям, а каждый из полученных интегралов вычисляется по формуле

или

Например, если левая или правая линии границы будут состоять из нескольких участков с различными уравнениями, то область 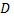 следует разбить прямыми, параллельными оси
следует разбить прямыми, параллельными оси 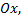 на части, где левая и правая линии границы определялись каждая одним уравнением. Таким образом, двойной интеграл по области
на части, где левая и правая линии границы определялись каждая одним уравнением. Таким образом, двойной интеграл по области 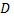 сводится к двум двукратным интегралам
сводится к двум двукратным интегралам

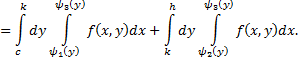
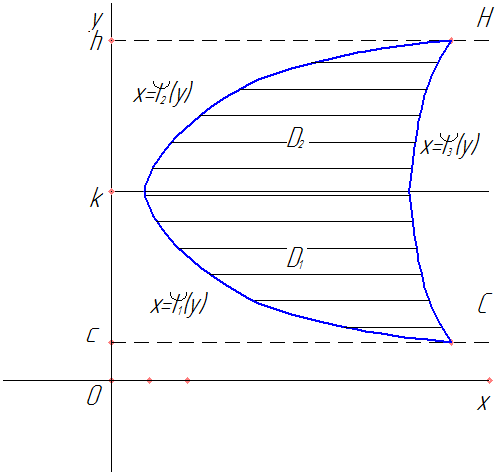
Рис. 50
Область интегрирования
Если окажется, что нижняя или верхняя линия границы состоит из нескольких участков, имеющих различные уравнения, то область  следует разбить прямыми, параллельными оси
следует разбить прямыми, параллельными оси  на части, в каждой из которых нижняя и верхняя линии определялись бы только одним уравнением. Тогда вычисление двойного интеграла сводится к вычислению двух двукратных интегралов
на части, в каждой из которых нижняя и верхняя линии определялись бы только одним уравнением. Тогда вычисление двойного интеграла сводится к вычислению двух двукратных интегралов


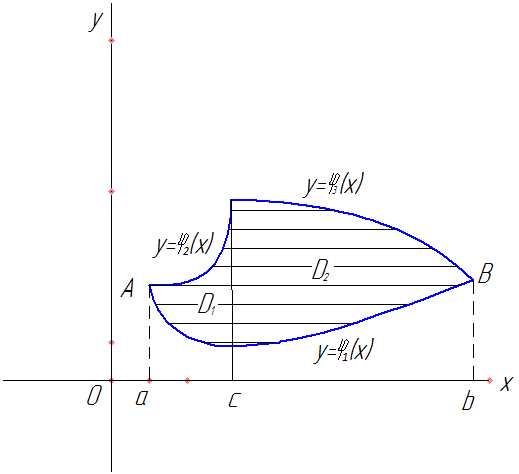
Рис. 51
Область интегрирования
Рассмотрим пример. Вычислить двойной интеграл

если область ограничена прямой 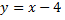 и параболой
и параболой 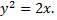
Построив данные линии между точками их пересечения  получим параболический сегмент
получим параболический сегмент 
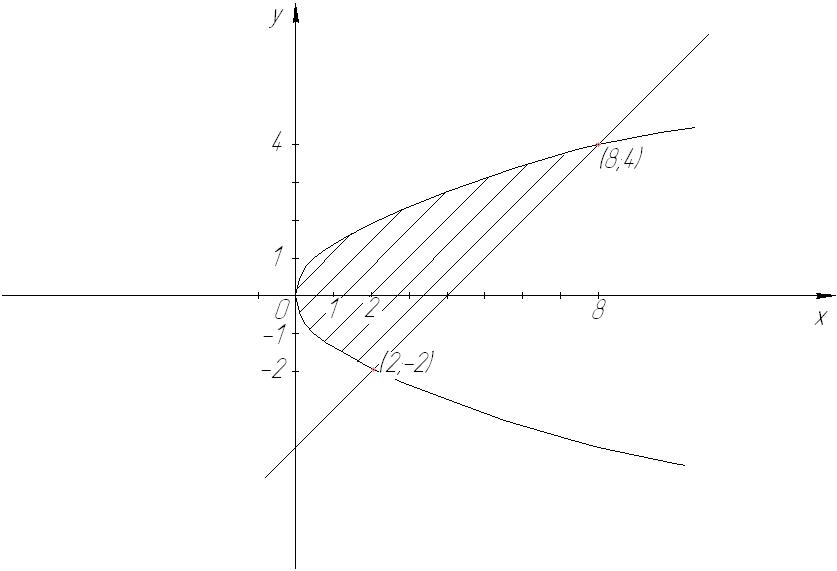
Рис. 52
Параболический сегмент
Если вначале интегрировать по  а затем по
а затем по 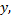 то двойной интеграл по этой области выражается двукратным интегралом
то двойной интеграл по этой области выражается двукратным интегралом
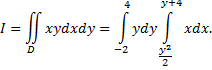
Точки 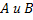 (с наибольшей и наименьшей ординатами) разбивают границу области на левую
(с наибольшей и наименьшей ординатами) разбивают границу области на левую  и правую
и правую  линии, каждая из которых определяется уравнением
линии, каждая из которых определяется уравнением
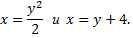
Вычисляя двукратный интеграл, получим

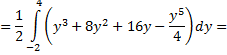
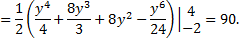
Если интегрировать в другом порядке – сначала по 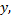 а затем по
а затем по  то необходимо разбить область интегрирования прямой
то необходимо разбить область интегрирования прямой  параллельно оси
параллельно оси 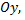 на две части, так как нижняя линия границы состоит из двух участков, которые имеют различные уравнения
на две части, так как нижняя линия границы состоит из двух участков, которые имеют различные уравнения
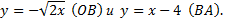
Вследствие этого вычисления несколько усложняются

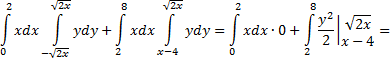
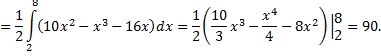
Рассмотрим пример. Изменить порядок интегрирования в интеграле
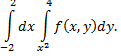
Вначале по пределам интегрирования определяем область интегрирования. Полагая  равным пределам интеграла с переменной
равным пределам интеграла с переменной  а
а  равным пределам интеграла с переменной
равным пределам интеграла с переменной 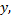 получим уравнения линий, ограничивающих эту область
получим уравнения линий, ограничивающих эту область


Рис. 53
Параболический сегмент
Построив эти линии, получим параболический сегмент  симметричный оси
симметричный оси 
Интегрируем вначале по  затем по
затем по  Пределы внутреннего интеграла находим, разрешая относительно
Пределы внутреннего интеграла находим, разрешая относительно  уравнение параболы
уравнение параболы
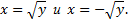
Пределы внешнего интеграла  находим как наименьшее и наибольшее значения
находим как наименьшее и наибольшее значения  по всей области
по всей области 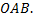 Следовательно
Следовательно
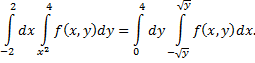
Двойной интеграл в полярных координатах.
В приложениях двойных интегралов к геометрическим и физическим задачам во многих случаях для упрощения вычислений полученный двойной интеграл, отнесенный к прямоугольным координатам, преобразуется к полярным координатам с помощью определенного правила. Правило следующее, для преобразования двойного интеграла, отнесенного к прямоугольным координатам, в двойной интеграл в полярных координатах нужно в подынтегральном выражении прямоугольные координаты заменить полярными
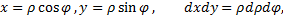

При этом уравнения линий, ограничивающих область интегрирования, также преобразуются к полярным координатам.
Если область 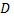 ограничена двумя лучами
ограничена двумя лучами  и
и 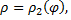 где
где  однозначные функции при
однозначные функции при
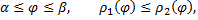
то двойной интеграл вычисляется по формуле
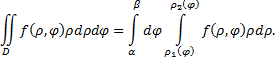
Переход в двойном интеграле к полярным координатам удобно использовать в тех случаях, когда подынтегральная функция зависит от  или от
или от 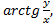 а также в тех случаях, когда граница области содержит дуги окружностей и лучи, выходящие из начала координат.
а также в тех случаях, когда граница области содержит дуги окружностей и лучи, выходящие из начала координат.
Рассмотрим пример. Преобразовать к полярным координатам и затем вычислить двойной интеграл

где  круговое кольцо, заключенное между окружностями
круговое кольцо, заключенное между окружностями

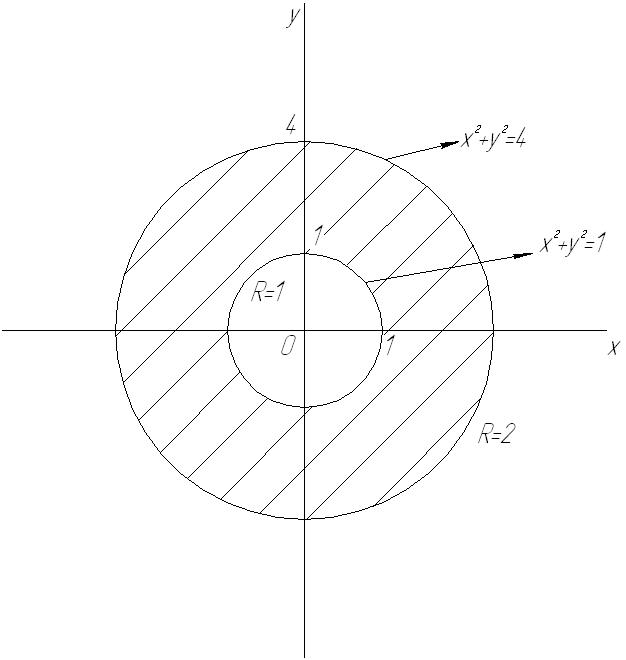
Рис. 54
Круговое кольцо
Пользуясь указанными правилами, получим
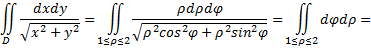

Контрольные вопросы
1. Сформулировать задачу интегрирования функции многих переменных.
2. Дать определение двойному интегралу.
3. Перечислить основные свойства двойного интеграла.
4. Какими способами интегрируют двойные интегралы?
Дата добавления: 2015-08-11; просмотров: 5786;
