Признак сходимости несобственных интегралов (признак сравнения)

Если функции и непрерывны на промежутке 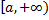и удовлетворяет на нем условию то из сходимости интеграла

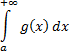
следует сходимость интеграла

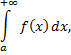
а из расходимости интеграла

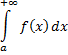
следует расходимость интеграла

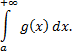
Рассмотрим пример. Исследовать сходимость

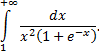
Сравним подынтегральную функцию

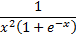
с функцией 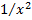на промежутке 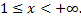Очевидно, что

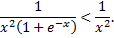
Но интеграл

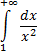
сходится, так как 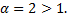Следовательно, согласно признаку сравнения сходится и данный интеграл.

Рассмотрим пример. Исследовать сходимость

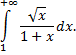
Сравнивая подынтегральную функцию

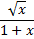
с функцией 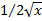на промежутке 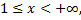имеем

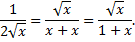
Но интеграл

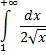
расходится, так как Следовательно, согласно признаку сравнения и данный интеграл сходится.

Контрольные вопросы

1. Дать определение несобственному интегралу с бесконечными пределами.

2. Дать определение несобственному интегралу с конечными пределами.

3. Какие несобственные интегралы называют сходящимися (расходящимися)?