Методы приближенного вычисления определенного интеграла
Понятие о приближенном вычислении определенных интегралов
Определенный интеграл
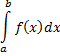
от заданной непрерывной функции 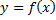 точно вычисляется далеко не всегда. Пользуясь геометрическим смыслом определенного интеграла можно дать ряд приближенных формул, с помощью которых этот интеграл находится с любой степенью точности. Рассмотрим простейшую из них, формулу трапеций.
точно вычисляется далеко не всегда. Пользуясь геометрическим смыслом определенного интеграла можно дать ряд приближенных формул, с помощью которых этот интеграл находится с любой степенью точности. Рассмотрим простейшую из них, формулу трапеций.
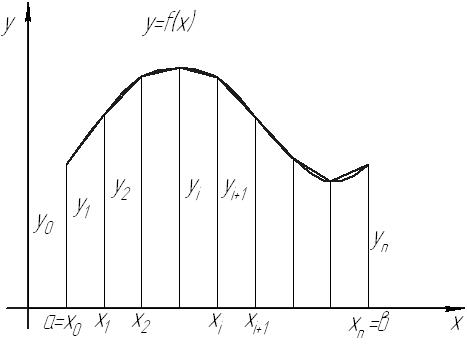
Рис. 46
Криволинейная трапеция
Определенный интеграл
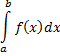
представляет собой площадь криволинейной трапеции, ограниченной линией 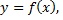 осью
осью 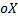 и двумя прямыми
и двумя прямыми 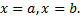
Разобьем отрезок  на
на  равных частей длины
равных частей длины
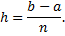
Пусть 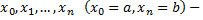 абсциссы точек деления и
абсциссы точек деления и  соответствующие ординаты кривой. Имеем расчетные формулы
соответствующие ординаты кривой. Имеем расчетные формулы
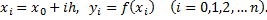
В результате построения криволинейная трапеция разбивается на ряд вертикальных полосок одной и той же ширины 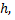 каждую из которых приближенно принимают за трапецию.
каждую из которых приближенно принимают за трапецию.
Суммируя площади этих трапеций, будем иметь

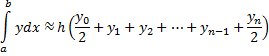
- это есть формула трапеций. Данную формулу можно записать в виде
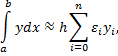
где  при
при 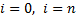 и
и  при
при 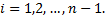
Ошибка
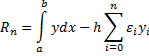
называется остаточным членом формулы трапеций.
Рассмотрим пример. Приближенно вычислить

Разобьем промежуток интегрирования 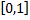 на 10 частей
на 10 частей 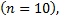 следовательно шаг
следовательно шаг 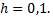
Абсциссы точек деления 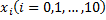 и соответствующие им ординаты
и соответствующие им ординаты
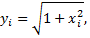 вычисленные с помощью таблицы квадратных корней, сводят в таблицу. Для удобства ординаты
вычисленные с помощью таблицы квадратных корней, сводят в таблицу. Для удобства ординаты 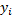 умножают на множитель
умножают на множитель 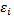 такой, что
такой, что  при
при 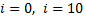 и
и 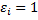 при
при 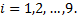
Таблица 7

| 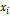
| 
|
| 0,0 | 0,5000 | |
| 0,1 | 1,0050 | |
| 0,2 | 1,0198 | |
| 0,3 | 1,0440 | |
| 0,4 | 1,0770 | |
| 0,5 | 1,1180 | |
| 0,6 | 1,1662 | |
| 0,7 | 1,2207 | |
| 0,8 | 1,2806 | |
| 0,9 | 1,3454 | |
| 1,0 | 0,7071 | |
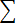
| 11,4838 |
Тогда, согласно формуле
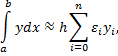
получим
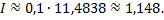
Точное значение интеграла равно
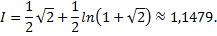
Контрольные вопросы
1. Перечислить геометрические приложения определенного интеграла.
2. Перечислить физические приложения определенного интеграла.
3. Сформулировать методы приближенного вычисления определенного интеграла.
Дата добавления: 2015-08-11; просмотров: 1898;
