Несобственные интегралы с бесконечными пределами интегрирования

В предыдущих лекциях мы рассматривали интегралы от функций, интегрируемых на конечных отрезках интегрирования. На практике возникает необходимость обобщения этих понятий на случаи, когда либо один из концов (или оба) отрезка интегрирования удален в бесконечность, либо функция не ограничена на отрезке интегрирования.

Пусть функция 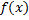определена на промежутке 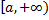и интегрируема по любому отрезку 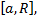т.е. существует определенный интеграл

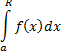
при любом 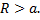Тогда, если существует конечный предел

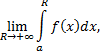
то его называют несобственным интегралом первого рода и обозначают

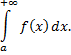
Таким образом, по определению,

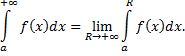
Если данный предел не существует или бесконечен, то несобственный интеграл не существует или расходится.

Аналогично вводится несобственный интеграл по промежутку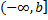

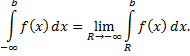
Несобственный интеграл с двумя бесконечными пределами можно определить как сумму выше рассмотренных несобственных интегралов

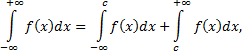
где -любое число, при условии существования обоих интегралов справа.

Геометрический смысл несобственного интеграла первого рода.

Пусть 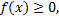тогда определенный интеграл

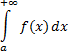
выражает площадь области, ограниченной сверху графиком функции 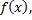снизу – осью 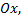слева – прямой 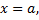справа – прямой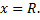

Несобственный интеграл

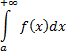
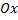выражает конечную площадь бесконечной области, ограниченной сверху графиком функции , снизу осью , слева прямой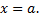

Рассмотрим пример вычисления несобственного интеграла первого рода.

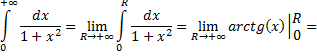
т.е. данный интеграл сходится.

Рассмотрим пример.

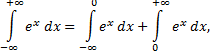
интеграл расходится, так как

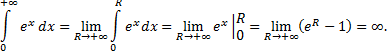
В рассмотренных примерах вычисление несобственного интеграла было основано на его определении.