Постановка задачи интегрирования функции многих переменных
В данной лекции рассматриваются вопросы, связанные с интегрированием функций нескольких переменных. В отличие от случая одной переменной здесь не удастся ввести простого понятия первообразной и неопределенного интеграла. В то же время определенный интеграл вводится аналогично: интегрирование рассматривается как «суммирование бесконечного числа бесконечно малых величин».
Пусть 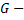 некоторая замкнутая ограниченная область, а
некоторая замкнутая ограниченная область, а 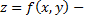 произвольная функция, определенная и ограниченная в этой области.
произвольная функция, определенная и ограниченная в этой области.
Предполагается, что граница области 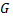 состоит из конечного числа кривых, заданных уравнениями
состоит из конечного числа кривых, заданных уравнениями 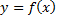 или
или 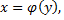 где
где  и
и 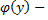 непрерывные функции. Такой областью, например, является замкнутый многоугольник, граница которого состоит из конечного числа отрезков, представляющих собой графики непрерывных функций
непрерывные функции. Такой областью, например, является замкнутый многоугольник, граница которого состоит из конечного числа отрезков, представляющих собой графики непрерывных функций 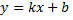 или
или 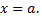
Разобьем область 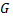 произвольно на
произвольно на  частей, не имеющих общих внутренних точек, с площадями
частей, не имеющих общих внутренних точек, с площадями 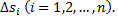 В каждой части
В каждой части 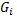 выберем произвольную точку
выберем произвольную точку  и составим сумму
и составим сумму

которую назовем интегральной суммой для функции  в области
в области 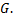
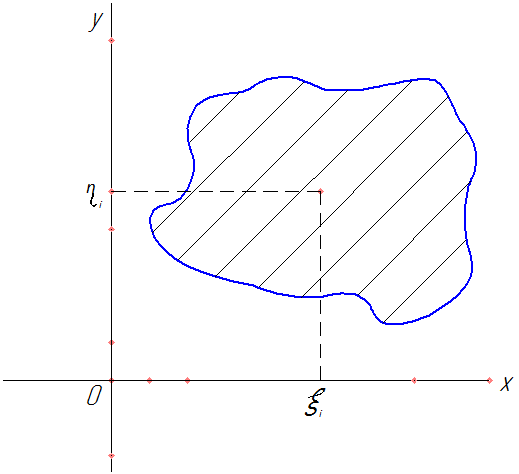
Рис. 47
Замкнутая ограниченная область
Дата добавления: 2015-08-11; просмотров: 809;
