Несобственные интегралы от неограниченных функций
Пусть функция 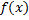 определена на промежутке
определена на промежутке 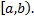 Точку
Точку 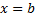 называют особой, если функция
называют особой, если функция 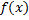 неограниченна в любой окрестности этой точки, но ограничена на любом отрезке
неограниченна в любой окрестности этой точки, но ограничена на любом отрезке  заключенном в
заключенном в 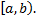 Пусть на любом отрезке
Пусть на любом отрезке 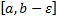 функция
функция  интегрируема, т.е. существует определенный интеграл
интегрируема, т.е. существует определенный интеграл
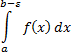
при любом  таком, что
таком, что 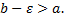 Тогда, если существует конечный предел
Тогда, если существует конечный предел
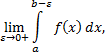
то его называют несобственным интегралом второго рода и обозначают
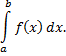
Если предел от данного интеграла не существует или бесконечен, то интеграл не существует и расходится.
Если 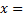 -особая точка, то несобственный интеграл определяется так
-особая точка, то несобственный интеграл определяется так
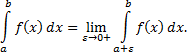
Если функция  не ограничена в окрестности какой-нибудь внутренней точки
не ограничена в окрестности какой-нибудь внутренней точки 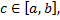 то при условии существования обоих интегралов справа по определению
то при условии существования обоих интегралов справа по определению
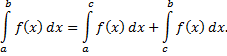
Если  -особые точки, то если оба интеграла справа существуют, несобственный интеграл определяется как сумма
-особые точки, то если оба интеграла справа существуют, несобственный интеграл определяется как сумма
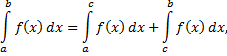
где 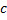 -любая точка из
-любая точка из 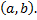
Дата добавления: 2015-08-11; просмотров: 946;
