Физические приложения определенного интеграла
Вычисление пройденного пути по скорости. Если 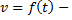 скорость движения материальной точки по некоторой прямой, то путь
скорость движения материальной точки по некоторой прямой, то путь  пройденный ею за промежуток времени
пройденный ею за промежуток времени 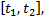 вычисляется по формуле
вычисляется по формуле
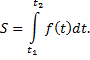
Рассмотрим пример. Материальная точка движется прямолинейно со скоростью
 (м/с). Найти путь, пройденный точкой за промежуток времени
(м/с). Найти путь, пройденный точкой за промежуток времени 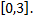
Согласно выше приведенной формуле, имеем
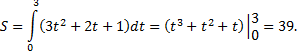
Вычисление работы переменной силы. Пусть под действием силы 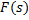 материальная точка
материальная точка 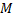 движется по прямой
движется по прямой 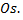 Работа этой силы на участке пути
Работа этой силы на участке пути  определяется по формуле
определяется по формуле
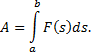
Рассмотрим пример. Вычислить работу, которую нужно затратить, чтобы растянуть пружину на 10 см, если известно, что для удлинения ее на 1 см необходимо приложить силу в 1 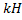 .
.
Согласно закону Гука, сила 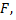 растягивающая пружину, пропорциональна ее растяжению, т.е.
растягивающая пружину, пропорциональна ее растяжению, т.е.
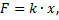
где 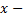 растяжение пружины (в метрах),
растяжение пружины (в метрах),  коэффициент пропорциональности. Так как по условию при
коэффициент пропорциональности. Так как по условию при  м сила
м сила 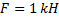 , то из равенства
, то из равенства
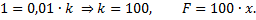
Следовательно искомая работа
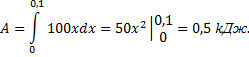
Вычисление моментов инерции.
С помощью определенного интеграла можно вычислять моменты инерции плоских фигур. Момент инерции материальной точки массой  относительно точки
относительно точки 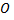 равен произведению массы этой точки на квадрат ее расстояния до точки
равен произведению массы этой точки на квадрат ее расстояния до точки 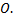 Момент инерции системы материальных точек равен сумме моментов инерции всех точек этой системы.
Момент инерции системы материальных точек равен сумме моментов инерции всех точек этой системы.
Вычислим момент инерции однородного круга массой  и радиусом
и радиусом  относительно его центра.
относительно его центра.
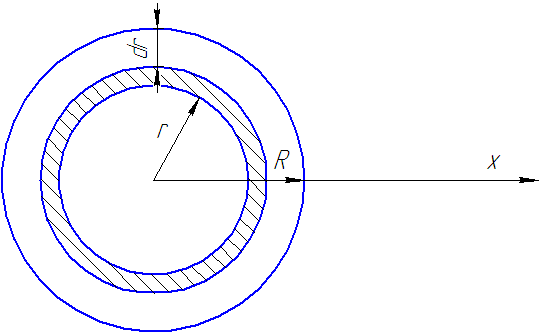
Рис. 44
Однородный круг заданной массы
Концентрическими окружностями с центром в точке 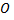 разобъем круг на
разобъем круг на  колец шириной
колец шириной 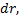 площадь каждого из которых
площадь каждого из которых
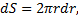
а масса

где плотность
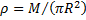 .
.
Элементарные моменты инерции выделенных колец
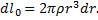
Суммируя (интегрируя) элементарные моменты инерции, получим
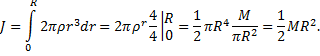
Вычисление координат центра тяжести плоской фигуры.
Координаты центра масс  плоской материальной дуги графика функции
плоской материальной дуги графика функции
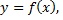 имеющей линейную плотность
имеющей линейную плотность 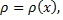 определяются по формулам
определяются по формулам
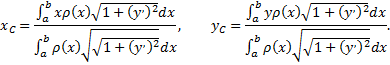
Если фигура ограничена снизу линией 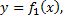 а сверху –
а сверху – 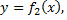 т.е.
т.е. 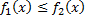 на отрезке
на отрезке 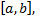 поверхностная плотность фигуры
поверхностная плотность фигуры 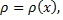 то вычисление ее центра масс
то вычисление ее центра масс 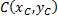 выполняется по по формулам
выполняется по по формулам
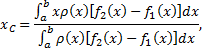
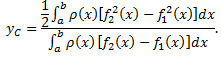
Рассмотрим пример. Вычислить координаты центра тяжести однородной плоской фигуры, ограниченной линиями
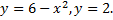
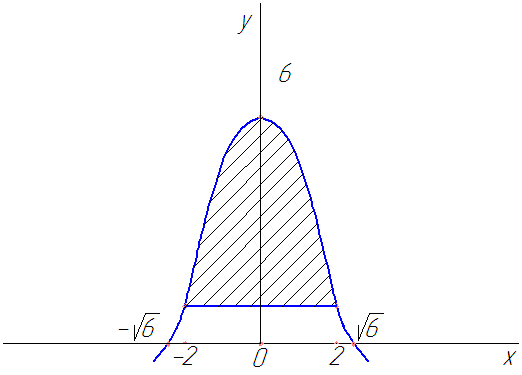
Рис. 45
Однородная плоская фигура
Из однородности и симметричности данной фигуры следует, что 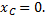 Для определения
Для определения 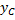 следует воспользоваться выше приведенными формулами
следует воспользоваться выше приведенными формулами
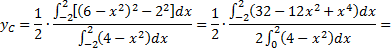
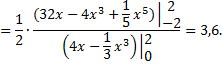
Дата добавления: 2015-08-11; просмотров: 7270;
