Формула Ньютона-Лейбница

Основная формула интегрального исчисления – формула Ньютона-Лейбница.

Если функция непрерывна на отрезке и 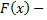одна из первообразных для на этом отрезке, то справедлива формула Ньютона-Лейбница

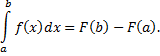
Правило вычисления определенного интеграла: определенный интеграл от непрерывной функции по отрезку равен разности значений произвольной ее первообразной функции в концах и отрезка

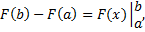
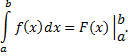
Рассмотрим пример:

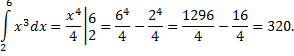
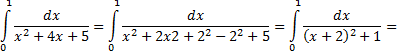
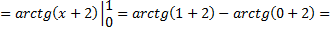
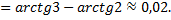
Пусть функция непрерывна на отрезке , а функция 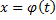имеет непрерывную производную на отрезке 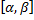таком, что:

1) множество значений функции совпадает с отрезком ;

2)

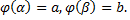
Тогда справедлива формула замены переменной в определенном интеграле

Рассмотрим пример:

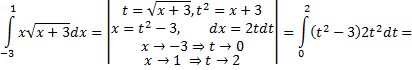
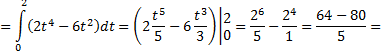
Пусть функци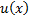и и 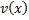имеют непрерывные производные на отрезке . Тогда справедлива формула

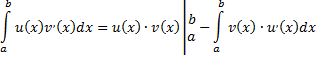
это есть формула интегрирования по частям в определенном интеграле.

Рассмотрим пример:

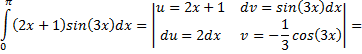
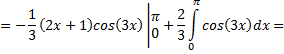
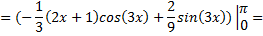
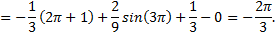
Контрольные вопросы

1. Что собой представляет интегральная сумма?

2. Какой вид имеет формула Ньютона-Лейбница?

3. Какими свойствами обладает определенный интеграл?

4. В чем состоит особенность метода замены переменной при его использовании для вычисления определенного интеграла?