Геометрические приложения определенного интеграла
Если функция  непрерывна и неотрицательна на отрезке
непрерывна и неотрицательна на отрезке  , то согласно геометрическому смыслу определенного интеграла, площадь криволинейной трапеции вычисляется по формуле
, то согласно геометрическому смыслу определенного интеграла, площадь криволинейной трапеции вычисляется по формуле
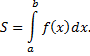
Если график расположен ниже оси 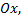 т.е.
т.е.  то площадь имеет знак « - », если график расположен выше оси
то площадь имеет знак « - », если график расположен выше оси 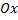 , т.е.
, т.е. 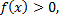 то площадь имеет знак «+». Для нахождения суммарной площади используют формулу
то площадь имеет знак «+». Для нахождения суммарной площади используют формулу

Площадь фигуры, ограниченной некоторыми линиями может быть найдена с помощью определенного интеграла, если известны уравнения этих линий.
+ +

 -
- 

Рис. 38
Рассмотрим пример.
Найти площадь фигуры, ограниченной параболой
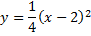
и прямой
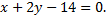
Площадь фигуры, ограниченной сверху непрерывной кривой 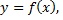 снизу – непрерывной кривой
снизу – непрерывной кривой 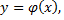 слева прямой
слева прямой 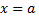 и справа прямой
и справа прямой 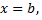 вычисляется по формуле
вычисляется по формуле
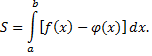
Определим точки пересечения данных линий. Из уравнения прямой находим
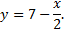
Теперь решим систему
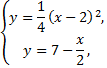

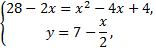
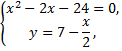
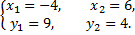
Таким образом, парабола и прямая пересекаются в точках 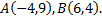 Так как сверху фигура ограничена прямой, а снизу – параболой, то, применяя известную формулу, получим
Так как сверху фигура ограничена прямой, а снизу – параболой, то, применяя известную формулу, получим
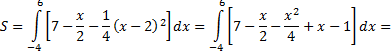
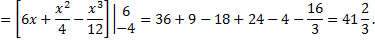
Полярная система координат.
Основная идея метода координат состоит в том, что положение точки на плоскости однозначно определяется с помощью двух чисел, геометрический смысл этих чисел дает ту или иную систему координат. Часто используется прямоугольная система координат и полярная система координат.
Возьмем на плоскости точку 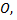 которую назовем полюсом. Проведем из полюса
которую назовем полюсом. Проведем из полюса 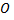 направленную полупрямую
направленную полупрямую 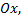 называемую полярной осью, и выберем масштаб для измерения длин
называемую полярной осью, и выберем масштаб для измерения длин
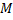

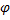
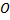
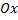
Рис. 39
Полярный радиус и полярный угол точки
Пусть точка 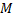 – произвольная точка плоскости. Соединим точку
– произвольная точка плоскости. Соединим точку 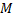 с полюсом
с полюсом 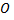 отрезком
отрезком 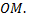 Длина отрезка
Длина отрезка 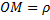 называется полярным радиусом точки
называется полярным радиусом точки 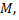 угол
угол 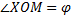 между полярной осью и вектором
между полярной осью и вектором 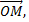 отсчитываемый против хода часовой стрелки, называется полярным углом точки
отсчитываемый против хода часовой стрелки, называется полярным углом точки 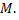
Полярными координатами точки 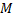 называется ее полярный радиус
называется ее полярный радиус  и полярный угол
и полярный угол 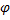 . Записывается так
. Записывается так  причем,
причем,

Между прямоугольными и полярными координатами существует связь. Для произвольной точки 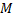 с прямоугольными координатами
с прямоугольными координатами  и
и 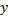 полярными координатами
полярными координатами  и
и 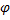 имеем
имеем
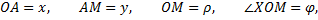
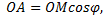

Прямоугольные координаты точки выражаются через ее полярные координаты по формулам
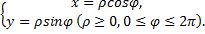
Зная прямоугольные координаты точки 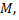 можно найти ее полярные координаты
можно найти ее полярные координаты 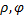 с помощью формул
с помощью формул
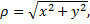
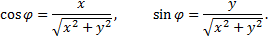
Рассмотрим пример.
Записать уравнение окружности 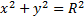 в полярных координатах. Используя вышеприведенные формулы, получим
в полярных координатах. Используя вышеприведенные формулы, получим

Таким образом, окружность радиуса  с центром в полюсе полярной системе координат задается уравнением
с центром в полюсе полярной системе координат задается уравнением
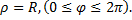
Вычисление длины дуги кривой.

Рис. 40
Дуга кривой
Пусть задана некоторая кривая. Разобьем ее на  частей точками
частей точками 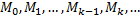 Рассмотрим вписанную ломаную, вершинами которой являются точки кривой, и обозначим через
Рассмотрим вписанную ломаную, вершинами которой являются точки кривой, и обозначим через 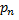 периметр этой ломаной, а через
периметр этой ломаной, а через 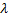 – длину наибольшего звена ломаной
– длину наибольшего звена ломаной

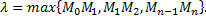
Если 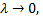 то длина каждого звена ломаной уменьшается, а их число
то длина каждого звена ломаной уменьшается, а их число  стремится к бесконечности.
стремится к бесконечности.
Если существует предел периметра 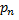 вписанной в кривую ломанной при
вписанной в кривую ломанной при  и этот предел не зависит от способа разбиения кривой на части, то указанный предел называется длиной дуги кривой и обозначается
и этот предел не зависит от способа разбиения кривой на части, то указанный предел называется длиной дуги кривой и обозначается 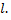 Кривая, имеющая длину, называется спрямляемой
Кривая, имеющая длину, называется спрямляемой
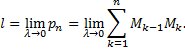
Если кривая задана в прямоугольной системе координат уравнением
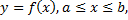
причем  непрерывна на отрезке
непрерывна на отрезке 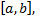 то кривая спрямляема и ее длина вычисляется по формуле
то кривая спрямляема и ее длина вычисляется по формуле
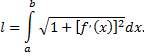
Рассмотрим пример. Найти длину кривой
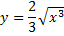
от начала координат до точки 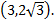
Так как
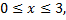
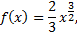

то
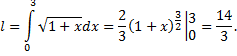
Пусть кривая задана в параметрической форме уравнениями

причем функции 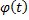 и
и 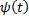 имеют непрерывные производные
имеют непрерывные производные 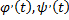 на отрезке
на отрезке 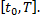 Тогда кривая спрямляема и ее длина вычисляется по формуле
Тогда кривая спрямляема и ее длина вычисляется по формуле
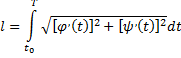
или
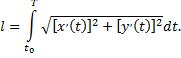
Вычисление объемов.
Пусть некоторое тело расположено между параллельными плоскостями 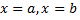 и пусть известна площадь любого его поперечного сечения
и пусть известна площадь любого его поперечного сечения 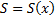 плоскостью, перпендикулярной оси
плоскостью, перпендикулярной оси 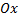 в точке с абсциссой
в точке с абсциссой 


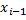
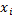

Рис. 41
Нахождение объема тела
Если функция 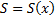 непрерывна на отрезке
непрерывна на отрезке  , то объем тела вычисляется по формуле
, то объем тела вычисляется по формуле
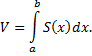
Недостатком этой формулы является то, что для нахождения объема необходимо знать функцию 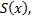 что весьма проблематично для сложных тел.
что весьма проблематично для сложных тел.
Рассмотрим пример.
Найти объем шара радиуса 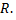
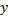
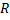

Рис. 42
В поперечных сечениях шара получаются окружности переменного радиуса  В зависимости от текущей координаты
В зависимости от текущей координаты  этот радиус выражается по формуле
этот радиус выражается по формуле
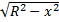 .
.
Тогда функция площадей сечений имеет вид
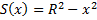 .
.
Получаем объем шара
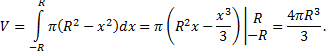
Объем тел вращения.
Рассмотрим кривую, заданную уравнением 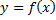 . Предположим, что функция
. Предположим, что функция  непрерывна на отрезке
непрерывна на отрезке  . Если соответствующую ей криволинейную трапецию с основаниями
. Если соответствующую ей криволинейную трапецию с основаниями  и
и 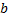 вращать вокруг оси
вращать вокруг оси 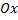 , то получим тело вращения.
, то получим тело вращения.
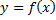

Рис. 43
Тело вращения
Так как каждое сечение тела плоскостью 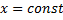 представляет собой круг радиуса
представляет собой круг радиуса  , то объем тела вращения может быть найден по формуле
, то объем тела вращения может быть найден по формуле
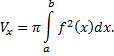
Аналогично можно вычислить объем тела, образованного вращением вокруг оси 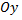 криволинейной трапеции, ограниченной графиком непрерывной неотрицательной функции
криволинейной трапеции, ограниченной графиком непрерывной неотрицательной функции 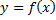 и прямыми
и прямыми
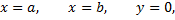
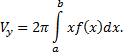
Дата добавления: 2015-08-11; просмотров: 1520;
