Свойства определенного интеграла. Теорема Коши о существовании определенного интеграла
Свойства определенного интеграла.
1)Если функция  определена в точке
определена в точке 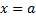 справедливо равенство
справедливо равенство
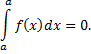
2)Если функция  интегрируема на отрезке
интегрируема на отрезке  , то
, то
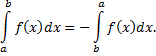
3)Интеграл
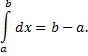
4)Если функция  интегрируема на отрезке
интегрируема на отрезке  и
и 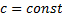 , то функция
, то функция 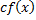 также интегрируема на отрезке
также интегрируема на отрезке  и справедливо равенство
и справедливо равенство
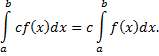
5)Если функции  интегрируемы на отрезке
интегрируемы на отрезке  , то функция
, то функция 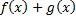 также интегрируема на отрезке
также интегрируема на отрезке  и справедливо равенство
и справедливо равенство

6)Если функция  интегрируема на отрезке
интегрируема на отрезке  и
и  то функция
то функция  интегрируема на отрезках
интегрируема на отрезках 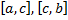 и справедливо равенство
и справедливо равенство
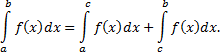
7)Если функция  интегрируема на отрезке
интегрируема на отрезке  и
и 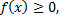 при всех
при всех 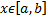 , то
, то

8)Если функции  интегрируемы на отрезке
интегрируемы на отрезке  и
и 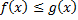 при всех
при всех 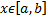 , то
, то
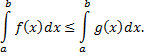
9)Если функция  интегрируема на отрезке
интегрируема на отрезке  и
и 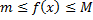 при всех
при всех 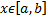 , то
, то

10)Если функция  интегрируема на отрезке
интегрируема на отрезке  и
и 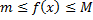 при всех
при всех 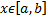 , то существует такое число
, то существует такое число 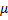 , удовлетворяющее неравенствам
, удовлетворяющее неравенствам 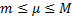 , что
, что
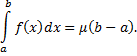
11)Если функция  интегрируема на отрезке
интегрируема на отрезке  , то на этом отрезке найдется такая точка
, то на этом отрезке найдется такая точка 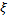 , что справедливо равенство
, что справедливо равенство

Определенный интеграл
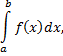
являющийся пределом интегральных сумм есть постоянная величина, не зависящая от того, какой буквой обозначена переменная интегрирования. Поэтому, если переменную  под знаком определенного интеграла обозначить другой буквой, то интеграл не изменится, т.е.
под знаком определенного интеграла обозначить другой буквой, то интеграл не изменится, т.е.
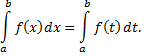
Достаточное условие существования определенного интеграла.
Если функция 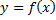 непрерывна на отрезке
непрерывна на отрезке  , то она интегрируема на этом отрезке.
, то она интегрируема на этом отрезке.
Дата добавления: 2015-08-11; просмотров: 1560;
