Квадратичные иррациональности

Интеграл вида

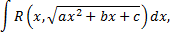
где 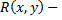рациональная функция относительно своих аргументов, всегда выражается через элементарные функции. При вычислении такого интеграла часто применяются тригонометрические подстановки. Для этого следует произвести дополнение до полного квадрата, в результате чего получится

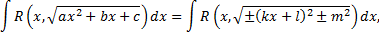
где 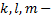постоянные. Затем делается подстановка

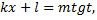
в случае ;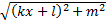

в случае ;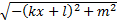

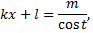
в случае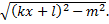

После этого корни извлекаются, и получается интеграл вида

где 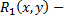новая рациональная функция относительно своих аргументов.

Интеграл от простейшей квадратичной иррациональности

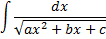
с помощью дополнения квадратного трехчлена до полного квадрата сводится к одному из двух интегралов

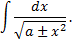
Первый интеграл

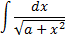
решается с помощью подстановки Эйлера

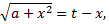
где 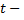новая переменная. После преобразований получим

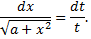
Таким образом,

Интеграл второго вида

Рассмотрим пример:

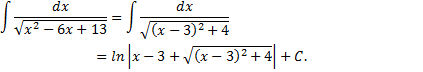
Рассмотрим пример:

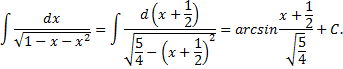
Контрольные вопросы

1. Для всякой ли иррациональной функции можно найти первообразную в виде элементарной функции?

2. При вычислении, каких интегралов применят тригонометрические подстановки?

3. Записать подстановки Чебышева. В каких случаях применят данные подстановки?