Линейные и дробно-линейные иррациональности
Рассмотрим интеграл вида
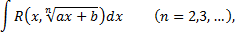
где 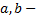 постоянные,
постоянные, 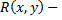 рациональная функция относительно своих двух аргументов. Тогда вся подынтегральная функция, рассмотренная как сложная функция от
рациональная функция относительно своих двух аргументов. Тогда вся подынтегральная функция, рассмотренная как сложная функция от  будет из-за наличия радикала иррациональной. Для рационализации этого интеграла совершим подстановку
будет из-за наличия радикала иррациональной. Для рационализации этого интеграла совершим подстановку
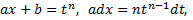
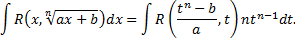
Полученная функция является рациональной.
Аналогичным образом, интеграл
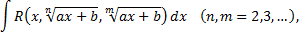
где 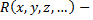 рациональная функция от своих аргументов, переходит в интеграл от рациональной функции после подстановки
рациональная функция от своих аргументов, переходит в интеграл от рациональной функции после подстановки 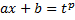 с соответственно подобранным
с соответственно подобранным 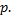
Рассмотрим пример:
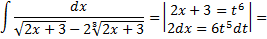

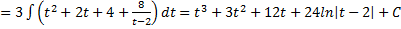 =
=
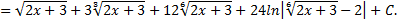
Рационализация интеграла
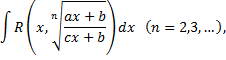
где 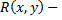 рациональная функция, осуществляется с помощью подстановки
рациональная функция, осуществляется с помощью подстановки
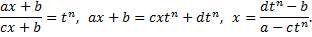
Не для всякой иррациональной функции можно найти первообразную в виде элементарной функции. Рассмотрим интегралы от некоторых иррациональных функций, которые с помощью определенных подстановок приводятся к интегралам от рациональных функций новой переменной.
Интеграл вида
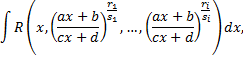
где 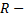 рациональная функция,
рациональная функция, 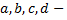 постоянные,
постоянные, 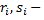 целые положительные числа,
целые положительные числа, 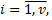 приводится к интегралу от рациональной функции новой переменной
приводится к интегралу от рациональной функции новой переменной 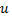 с помощью подстановки
с помощью подстановки
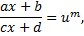
где число 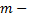 наименьшее общее кратное знаменателей дробей
наименьшее общее кратное знаменателей дробей
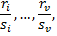
т.е. 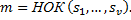
Интеграл вида
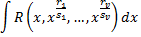
приводится к интегралу от рациональной функции новой переменной 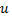 с помощью подстановки
с помощью подстановки 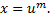
Рассмотрим пример:
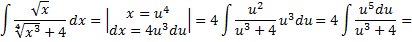
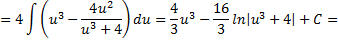
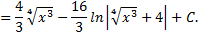
Рассмотрим еще один пример:
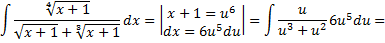
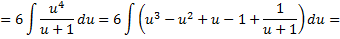

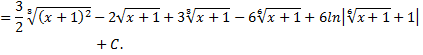
Интеграл вида
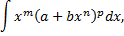
где 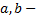 постоянные, отличные от нуля,
постоянные, отличные от нуля, 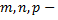 рациональные числа, можно привести к интегралу от рациональной функции с помощью подстановок Чебышева в трех случаях:
рациональные числа, можно привести к интегралу от рациональной функции с помощью подстановок Чебышева в трех случаях:
1) если 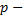 целое число, то имеем случай интегрирования простейших иррациональных функций;
целое число, то имеем случай интегрирования простейших иррациональных функций;
2) если
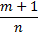
- целое число, то применяется подстановка
 ;
;
3) если
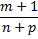
- целое число, то используется подстановка 
Рассмотрим пример:
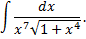
Так как  то
то
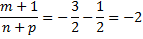
- целое число. Тогда
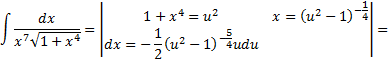
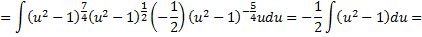
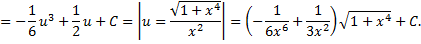
Дата добавления: 2015-08-11; просмотров: 1612;
