Интегрирование с помощью универсальных подстановок

Интегралы вида

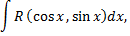
где 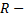рациональная функция, приводятся к интегралам от рациональных функций новой переменной 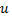с помощью универсальной подстановки

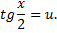
В этом случае

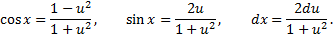
Интегралы вида

где 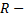рациональная функция, приводятся к интегралам от рациональных функций новой переменной 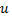с помощью упрощенной подстановки

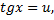
при этом

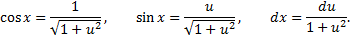
Рассмотрим пример:

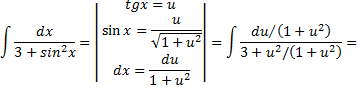
Рассмотрим пример:

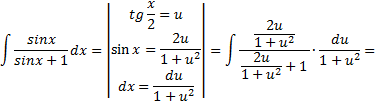
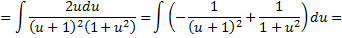
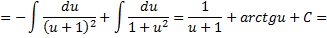
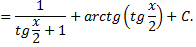
Рассмотрим пример:

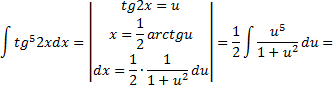
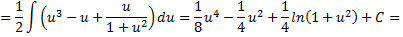
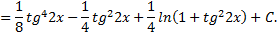
Рассмотрим пример:

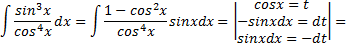
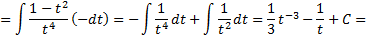
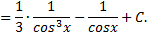
Контрольные вопросы

1. В каких случаях применяют метод замены переменной в интегрировании?

2. С помощью какого метода находят интегралы от обратных тригонометрических функций?

3. С помощью, какой универсальной подстановки находят интегралы, содержащие тригонометрические функции?