IV. ИНТЕГРИРОВАНИЕ НЕКОТОРЫХ ИРРАЦИОНАЛЬНОСТЕЙ
Основным методом решения интегралов от иррациональных выражений является метод замены переменной.
Цель замены – преобразовать данное иррациональное выражение к рациональной дроби.
1. 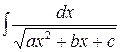 сводится к
сводится к 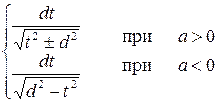 ,
,
предварительно необходимо выделить полный квадрат под знаком корня, сделать замену и проинтегрировать по таблице интегралов, 10 и 12.
Пример 28.
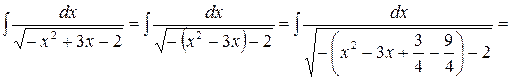
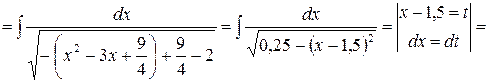
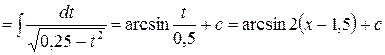 .
.
2. 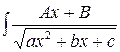
1) Сделать в числителе производную подкоренного выражения.
2) Разбить на два интеграла, один из которых степенной, а другой вида (1).
Пример 29.
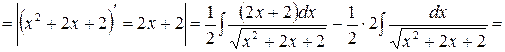
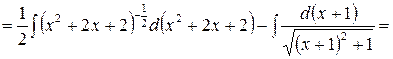
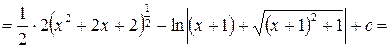
 .
.
3. 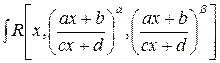 подстановка
подстановка 
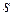 – наименьший общий знаменатель дробей
– наименьший общий знаменатель дробей 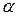 и
и  .
.
Пример 30. 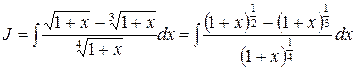
Здесь роль 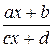 играет
играет 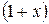 ,
, 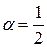 ;
; 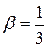 ;
; 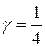 , наименьший общий знаменатель этих дробей
, наименьший общий знаменатель этих дробей 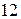 , следовательно, подстановка
, следовательно, подстановка  , вычислим
, вычислим 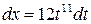
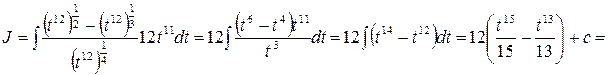
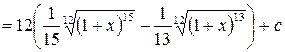 .
.
4. 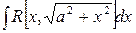 ,
, 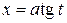 ;
;
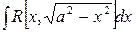 ,
, 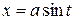 ;
;
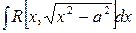 ,
, 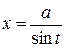 .
.
5. 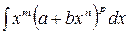 – дифференциальный бином интегрируется в трех случаях:
– дифференциальный бином интегрируется в трех случаях:
1) 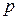 – целое,
– целое, 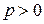 – интегрируется непосредственно,
– интегрируется непосредственно,
 – подстановка
– подстановка 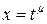 , где
, где 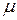 – общий знаменатель дробей
– общий знаменатель дробей
 и
и 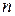 ;
;
2) 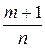 – целое (
– целое ( 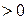 ,
, 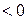 ,
, 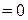 ) подстановка
) подстановка 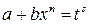 , где
, где 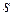 – знаменатель
– знаменатель
дроби 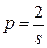 ;
;
3)  – целое (
– целое ( 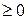 ,
, 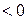 ,) подстановка
,) подстановка 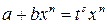 .
.
Пример 31. 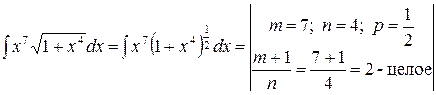
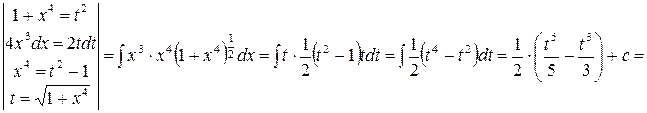
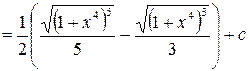 .
.
Дата добавления: 2015-08-11; просмотров: 1742;
