ИХ ВЫЧИСЛЕНИЕ
Если 1) 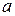 и
и 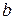 конечны;
конечны;
2) 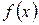 непрерывна на
непрерывна на 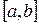 и имеет первообразную
и имеет первообразную 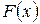 , то определенный интеграл выражается конечным числом и может быть вычислен по формуле Ньютона-Лейбница:
, то определенный интеграл выражается конечным числом и может быть вычислен по формуле Ньютона-Лейбница:
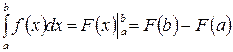 . (7)
. (7)
Пример 40. 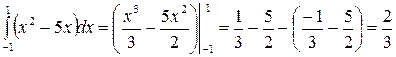 .
.
Интегралы а) 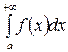 ; б)
; б) 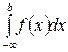 ; в)
; в) 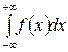
относятся к несобственным интегралам I-го рода, т. к. для них не выполнено условие (1), а именно: один из пределов интегрирования (случая а) и б) ) или оба (случай в) ) не являются конечными, а условие (2) выполнено. Вычисление таких интегралов можно проводить по формуле (7), при этом 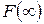 считается как предельное значение, которое может быть конечным, бесконечным или не иметь смысла.
считается как предельное значение, которое может быть конечным, бесконечным или не иметь смысла.
Пример 41. 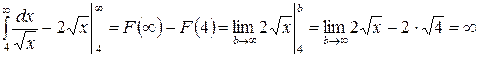 .
.
Пример 42. 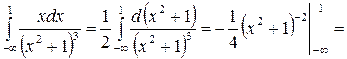
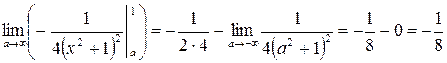 .
.
Пример 43. 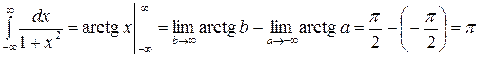 .
.
Если в результате вычислений получили конечное число, то несобственный интеграл называется сходящимся (примеры 42, 43), в противном случае интеграл расходится (пример 41).
Те интегралы 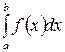 , для которых не выполняется условие (2), а условие (1) выполнено, относятся к несобственным интегралам II-го рода.
, для которых не выполняется условие (2), а условие (1) выполнено, относятся к несобственным интегралам II-го рода. 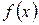 имеет бесконечный разрыв в одной или нескольких точках.
имеет бесконечный разрыв в одной или нескольких точках.
Вычисление несобственных интегралов II-го рода и определение их сходимости или расходимости можно проводить по формуле Ньютона-Лейбница, определив точки бесконечного разрыва.
Пример 44. 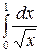 ;
; 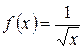 ; эта функция имеет бесконечный разрыв на
; эта функция имеет бесконечный разрыв на 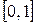 в точке
в точке 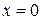 , т. к.
, т. к. 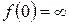 .
.
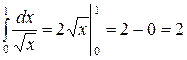 , интеграл сходится.
, интеграл сходится.
Пример 45. 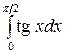 ;
; 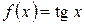 имеет бесконечный разрыв на
имеет бесконечный разрыв на 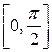 в точке
в точке 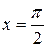 , т. к.
, т. к. 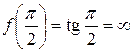 .
.
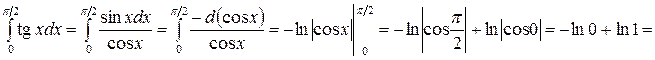
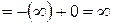 , интеграл расходится.
, интеграл расходится.
Пример 46. 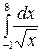 ;
; 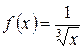 имеет бесконечный разрыв в точке
имеет бесконечный разрыв в точке 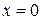 , которая принадлежит
, которая принадлежит 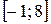 . В этом случае данный интеграл разбиваем на два интеграла точкой разрыва:
. В этом случае данный интеграл разбиваем на два интеграла точкой разрыва:
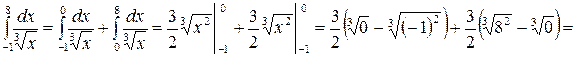
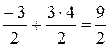 , интеграл сходится.
, интеграл сходится.
| Геометрические приложения определенного интеграла | ||||
| Система координат | Вид уравнения кривой | Площадь плоской фигуры | Длина дуги | Объем тела вращения |
| Декартовы координаты | а)
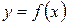
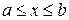
| 1а)
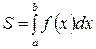
| 2а)
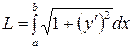
| 3а)
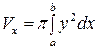
|
б)
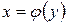
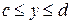
| 1б)
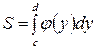
| 2б)
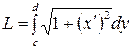
| 3б)
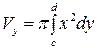
| |
в)
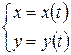
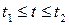
| 1в)

| 2в)

| 3в)
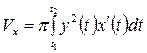 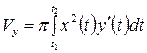
| |
г)

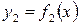
| 1г)
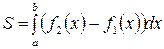
| 2г)
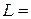
| 3г) | |
| Полярные координаты | д)
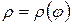
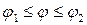
| 1д)
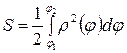
| 2д)
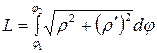
| 3д)
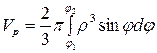
|
Дата добавления: 2015-08-11; просмотров: 1063;
