ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
При помощи определенного интеграла можно вычислить площади плоских фигур, длины дуг, объемы тел вращения, а также решать другие задачи.
В зависимости от того, в какой системе координат решается задача и в каком виде задано уравнение кривой, выбирается нужная формула по таблице.
Для определения пределов интегрирования необходимо сделать чертеж. Затем подставить в формулу конкретные данные своей задачи и провести вычисления.
Пример 47. Вычислить площадь, ограниченную параболой  и прямыми
и прямыми 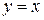 и
и 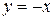 .
.
Решение: Выполним чертеж. Графиком  является парабола,
является парабола,

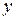 ветви которой направлены
ветви которой направлены
вниз (знак “ - “ перед  ) и
) и
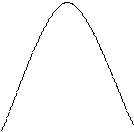
 приподняты на 2 единицы
приподняты на 2 единицы
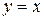
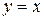 (рис. 1).
(рис. 1).
Искомая площадь симметрична
относительно оси 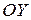 ,
,
следовательно, можно

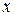 вычислить половину площади
вычислить половину площади
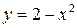 и удвоить результат.
и удвоить результат.
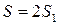 .
.
Рис. 1
Для вычисления пределов интегрирования решим совместное уравнение параболы и прямой 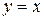 :
:
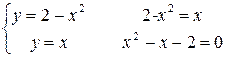
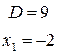
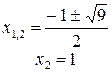 ,
,
согласно формуле (1г), табл. получим
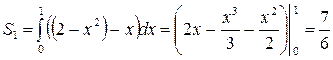 ;
; 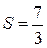 (кв. ед.)
(кв. ед.)
Пример 48. Вычислить площадь, ограниченную линией
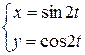 ,
, 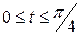 .
.
Решение: В данной задаче чертеж выполнять необязательно, т. к. задано изменение параметра  . Уравнение линии рассматривается в декартовых координатах, но имеет параметрический вид (в). Воспользуемся формулой (1в) табл.
. Уравнение линии рассматривается в декартовых координатах, но имеет параметрический вид (в). Воспользуемся формулой (1в) табл.

 .
.
Пример 49. Вычислить площадь, ограниченную линией 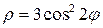 .
.
Решение: Так как уравнение линии, ограничивающей искомую площадь, задано в полярных координатах, то необходимо воспользоваться формулой (1д), табл.
Пределы интегрирования не заданы,
поэтому необходимо сделать чертеж
(рис. 2). Линию 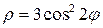
построим по точкам, давая  значения
значения
через равный промежуток, например,
 , начиная от
, начиная от 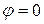 до
до 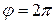 .
.
Вычислим 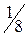 искомой площади.
искомой площади.
Рис. 2
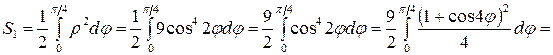
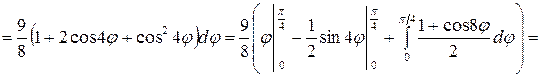
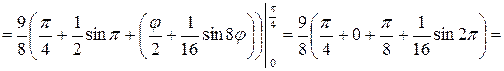
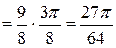
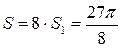 (кв. ед.).
(кв. ед.).
Пример 50. Найти длину дуги 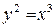 , отсеченную прямой
, отсеченную прямой 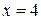 .
.
Решение: Уравнение линий заданы в декартовых координатах.

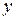 Воспользуемся формулой (2а),
Воспользуемся формулой (2а),
 табл.
табл. 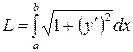 .
.
Дата добавления: 2015-08-11; просмотров: 992;
