Вычисление площади с помощью криволинейного интеграла ІІ рода
План
- Вычисление площади с помощью криволинейного интеграла ІІ рода
- Условия независимости криволинейного интеграла ІІ рода от пути интегрирования. Признак точного дифференциала
Вычисление площади с помощью криволинейного интеграла ІІ рода
Нужно вычислить площадь криволинейной трапеции 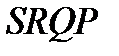 (рис.1), при этом
(рис.1), при этом 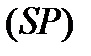 и
и 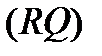 могут быть стянутыми в точки. Кривые
могут быть стянутыми в точки. Кривые 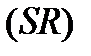 и
и 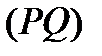 задаются следующим образом:
задаются следующим образом:
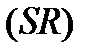 :
:  ,
, 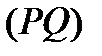 :
: 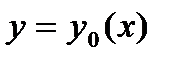 ,
, 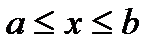 ,
,
и они такие, что любая прямая, параллельная ОУ ( 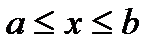 )пересекает каждую из них в одной точке. Такую криволинейную трапецию будем называть трапецией І типа.
)пересекает каждую из них в одной точке. Такую криволинейную трапецию будем называть трапецией І типа.
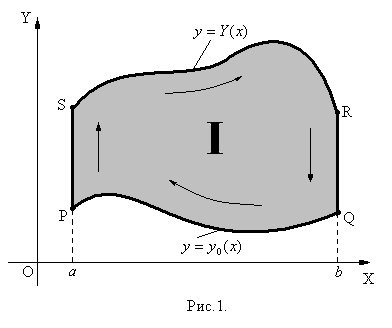
Как известно из темы «Применение интеграла Римана», площадь криволинейной трапеции 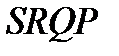 определяется при помощи формулы:
определяется при помощи формулы:
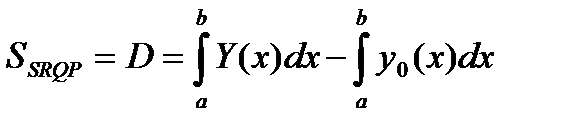 . (10)
. (10)
С другой стороны:
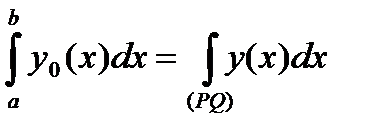 ,
,  ,
,
Тогда
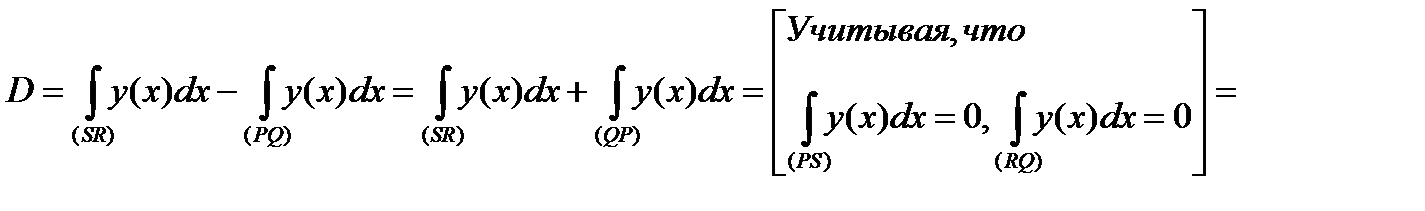
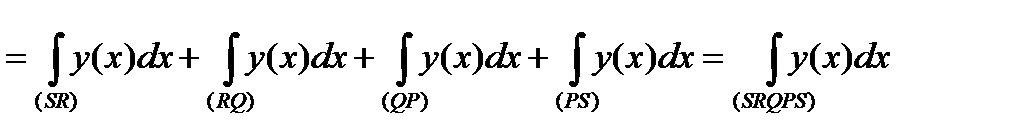 . (20)
. (20)
Пусть  - это контур
- это контур 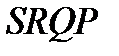 . Выберем положительное направление обхода этого контура (противоположное тому направлению, которое изображено на рис.1), тогда из формулы (20) имеем, что площадь криволинейной трапеции І типа может быть вычислена по формуле:
. Выберем положительное направление обхода этого контура (противоположное тому направлению, которое изображено на рис.1), тогда из формулы (20) имеем, что площадь криволинейной трапеции І типа может быть вычислена по формуле:
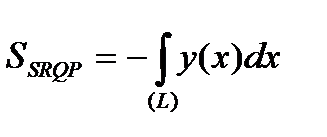 . (30)
. (30)
Рассмотрим криволинейную трапецию 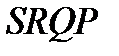 ІІ типа (рис.2), которая определяется
ІІ типа (рис.2), которая определяется
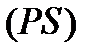 :
: 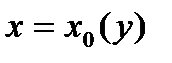 ,
,  :
:  ,
, 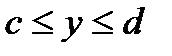 ,
,
а 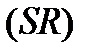 и
и 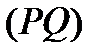 могут быть стянутыми в точки. Кривые
могут быть стянутыми в точки. Кривые 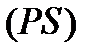 и
и  такие, что любая прямая, параллельная ОХ (
такие, что любая прямая, параллельная ОХ ( 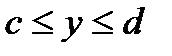 ) пересекает каждую из них в одной точке. Кривая
) пересекает каждую из них в одной точке. Кривая  - это контур
- это контур 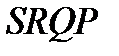 .
.
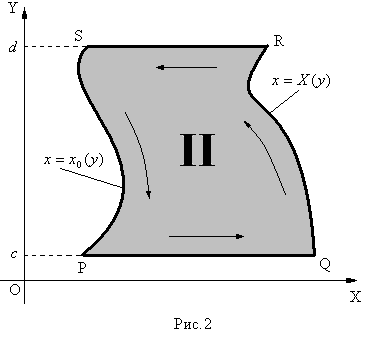
Тогда аналогично тому, как это было сделано выше для криволинейной трапеции І типа, можно показать, что площадь криволинейной трапеции ІІ типа может быть вычислена с помощью формулы:
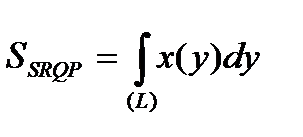 . (40)
. (40)
Некоторые области одновременно можно рассматривать как криволинейные трапеции и І, и ІІ типа (например, область на рис.3). В этом случае для вычисления площади такой фигуры подходят обе формулы: (30) и (40). Если эти формулы почленно сложить и поделить на 2, то получим еще одну формулу для вычисления площади фигуры, которая одновременно является криволинейной трапецией и І, и ІІ типа, в виде криволинейного интеграла общего вида:
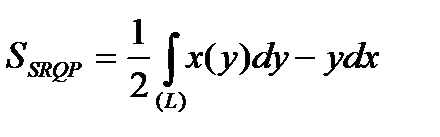 . (50)
. (50)

Пусть теперь нужно вычислить площадь плоской фигуры, которая не является криволинейной трапецией ни І, ни ІІ типа (например, фигура, которая представлена на рис.4). В этом случае представленную фигуру разбивают прямыми, параллельными осям координат, на части, каждая из которых будет криволинейной трапецией І или ІІ типа (рис.4). Площадь каждой части вычисляют, пользуясь одной из формул (30), (40), (50). Площадь всей фигуры будет равна сумме площадей всех ее частей.
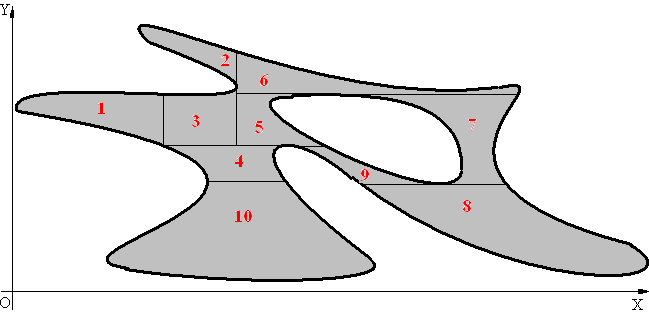
Рис.4.
Пример. Найти площадь эллипса, параметрическое задание которого, как известно, выглядит следующим образом:
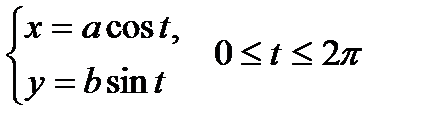 .
.
Поскольку эллипс является одновременно как криволинейной трапецией І, так и ІІ типа, для вычисления его площади можно воспользоваться формулой, например, (50):
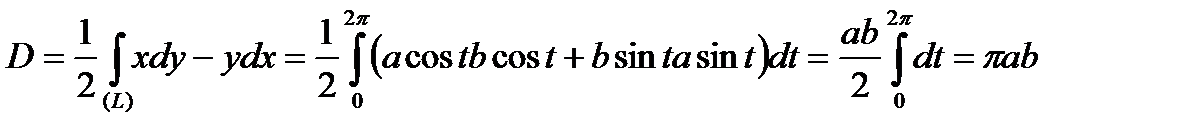 .
.
Дата добавления: 2015-08-21; просмотров: 3427;
