Условия независимости криволинейного интеграла ІІ рода от пути интегрирования. Признак точного дифференциала

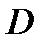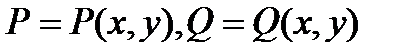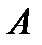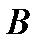Пусть - некоторая связная область. Пусть на этой области определены непрерывные функции . Пусть и - две произвольные точки из области 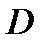, 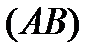- произвольная кривая, которая соединяет 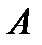и 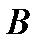и полностью находится в .

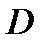Вопрос: Когда значение интеграла

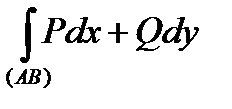(60)

не зависит от формы пути 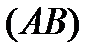, т.е. однозначно определяется только точкам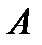и и ?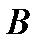

Теорема. Для того, чтобы интеграл (60) не зависел от пути интегрирования, необходимо и достаточно, чтобы дифференциальное выражение 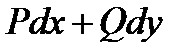было в области 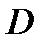дифференциалом от некоторой функции :

,

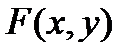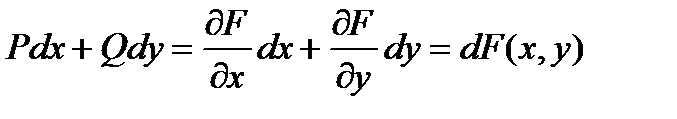т.е. .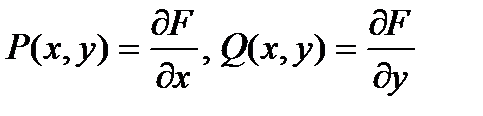

Пусть в области 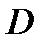непрерывны не только сами функци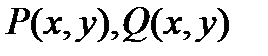и , а и 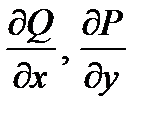. Если 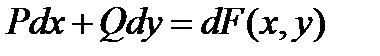, т.е. 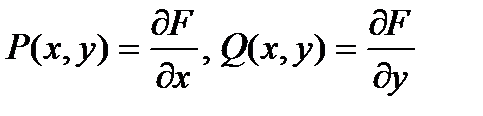, то

.

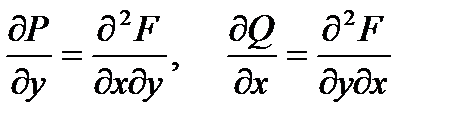Поскольку 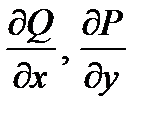- непрерывны, то непрерывны и смешанные производные второго порядка 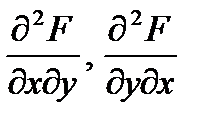, а потому 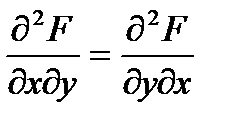, из чего следует:

. (70)

Условие (70) - это необходимое условие того, чтобы выражение 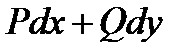было в области 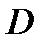полным дифференциалом. Можно показать, что (70) – это и достаточное условие в случае односвязности 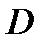. Таким образом, имеет место следующая теорема.

Теорема. Для того, чтобы криволинейный интеграл ІІ рода (60), где бы в области 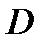не были взяты точк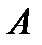и и 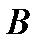, не зависел от формы пути 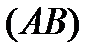, необходимо, а если 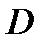- односвязная обасть, и достаточно, чтобы выполнялось условие (70).

Вопросы

1. Как вычисляется площадь криволинейной трапеции с помощью интеграла Римана?
2. Какая криволинейная трапеция называется трапецией І типа (ІІ типа)?
3. Как вычисляется площадь криволинейной трапеции І типа (ІІ типа) с помощью криволинейного интеграла ІІ рода?
4. Как вычисляется площадь криволинейной трапеции, которая одновременно является трапецией І і ІІ типа, с помощью криволинейного интеграла ІІ рода?
5. Как вычисляется площадь плоской области, которая не является криволинейной трапецией?
6. Когда значение криволинейного интеграла ІІ рода не зависит от пути интегрирования?