Вычисление объемов тел и площадей плоских фигур при помощи двойного интеграла

Вычисление объема тела. Объем цилиндрического тела, ограниченного сверху непрерывной поверхностью z = f (x, y), снизу плоскостью z = 0 и сбоку прямой цилиндрической поверхностью, вырезающей на плоскости хОу область D, вычисляется по формуле

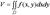
При z = f (x, y) < 0 объем цилиндрического тела вычисляется по формуле

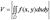, т.е. равен модулю двойного интеграла.

Вычисление площади плоской фигуры. Площадь плоской фигуры, ограниченной областью D, находится по формуле

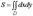(1)

Если область определена в прямоугольной системе координат неравенством 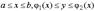, то из ур-я (1) имеем

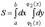
Если область D определена в полярных координатах неравенством 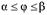, , 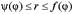то

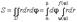
Пример:

V=

V=

f₂(x,y)-V от f₂ до плоскости y

f₁(x,y)-V от плоскости до лица.

S=

; f(x,yz)=1;