Нахождение коэффициентов
I способ.
Пусть 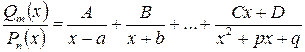 ,
, 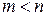 ,
, 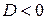 .
.
Написанное равенство есть тождество, а поэтому:
а) приведя дроби к общему знаменателю, получим тождественные многочлены в числителях справа и слева;
б) приравняем числители;
в) а затем их коэффициенты при одинаковых степенях;
г) получим систему уравнений для определения коэффициентов.
Пример 25. Рассмотрим пример 21.
а) Приведем дробь к общему знаменателю:
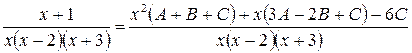 .
.
б) Приравняем числители:
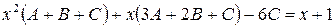 .
.
в) Приравняем коэффициенты при одинаковых степенях:
|
|
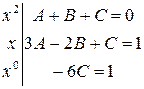 (коэффициент при
(коэффициент при 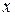 )
)
г) Решив систему, получим:
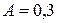 ;
; 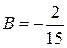 ;
; 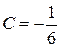 .
.
Получили разложение
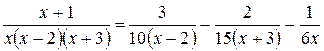 .
.
II способ.
Приравняем многочлены в числителях слева и справа, как в I способе:
д) Придадим 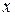 частные значения, вычислим значения многочленов. Получим также систему с неизвестными коэффициентами.
частные значения, вычислим значения многочленов. Получим также систему с неизвестными коэффициентами.
В качестве значений 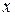 удобно брать значения действительных корней знаменателя, лучше применять в случае, когда знаменатель имеет равные действительные корни.
удобно брать значения действительных корней знаменателя, лучше применять в случае, когда знаменатель имеет равные действительные корни.
Пример 26. 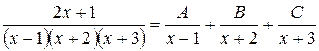 ,
,
а) 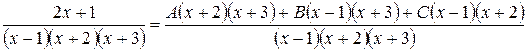
б) 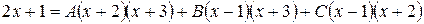
д) 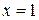

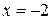
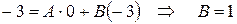
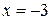
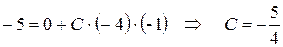
В итоге 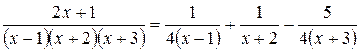 .
.
III способ.
Комбинируют I и II способы.
Дата добавления: 2015-08-11; просмотров: 1345;

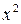 )
)