Значения коэффициентов Стьюдента
| n δ | 0,9 | 0,95 | 0,99 | 0,999 |
| ∞ | 6,31 2,92 2,35 2,13 2,02 1,94 1,90 1,86 1,83 1,65 | 12,71 4,30 3,18 2,78 2,57 2,45 2,36 2,31 2,26 1,96 | 63,66 9,92 5,84 4,60 4,03 3,71 3,50 3,36 3,25 2,58 | 636,62 31,60 12,84 8,61 6,86 5,96 5,40 5,04 4,78 3,29 |
Например, задавая доверительную вероятность δ =0.95, по числу проведенных измерений n=5 по табл. 2 можно найти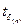 
= 2,78. Тогда, определив предварительно 
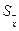по формуле (35), найдем погрешность ∆X:
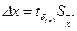(41)
Выражение (41) ввиду малого объема информации дает границы доверительного интервала более широкими.
Результат измерения можно представить в виде:
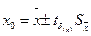при δ=0,95, n=5. (42)
Конечно, оценка (42) еще не дает представления об общей погрешности измерения, в которую входит и систематическая ошибка.
Совместный учет случайных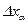 
и систематических 
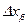ошибок можно произвести по формуле
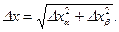
При этом следует принять во внимание, что 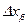всегда имеет максимальное значение. Максимальное же значение случайных ошибок равно 3σ . Следовательно, для их равноправного учета необходимо предположить, что приборная погрешность β (или ∆пр) равна утроенной дисперсии распределения погрешностей прибора 3σпр ,т.е. погрешности соответствующей надежности δ =0.997. Тогда за систематическую ошибку можно принять 
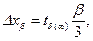и общая погрешность выразится соотношением
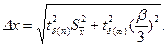(43)
Коэффициенты Стьюдента для проведенного числа измерений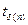 
и бесконечного числа измерений 
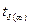находят по табл.2 для одной и той же заданной надежностиδ.
Дата добавления: 2015-08-01; просмотров: 1549;