Выборочной метод
В классическом методе для нахождения границ доверительного интервала 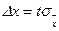 при заданной надежности δ или наоборот, для определения δ по заданному ΔХ необходимо знать точное значение дисперсии σ2 генеральной совокупности измерений. Из опытных данных нам известна лишь дисперсия
при заданной надежности δ или наоборот, для определения δ по заданному ΔХ необходимо знать точное значение дисперсии σ2 генеральной совокупности измерений. Из опытных данных нам известна лишь дисперсия 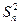 случайной выборки из этой генеральной совокупности. А так как рассеяние результатов относительно средней арифметической
случайной выборки из этой генеральной совокупности. А так как рассеяние результатов относительно средней арифметической  всегда меньше рассеяния относительно истинного значения Х0, то
всегда меньше рассеяния относительно истинного значения Х0, то 
Если мы для оценки доверительного интервала или доверительной вероятности воспользуемся табл.2 интеграла вероятностей, полагая 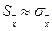 при малом числе измерений п, то найдем неверные значения ΔХ (заниженные) и δ (завышенные). В этом заключается недостаток классического метода оценки точности результата измерений.
при малом числе измерений п, то найдем неверные значения ΔХ (заниженные) и δ (завышенные). В этом заключается недостаток классического метода оценки точности результата измерений.
Оказывается, что и при неизвестной дисперсии σг можно дать точную оценку приближенного равенства Хр 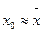 , если исходить не из распределения величины
, если исходить не из распределения величины 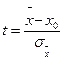 , а из распределения другой случайной величины
, а из распределения другой случайной величины
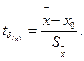 (38)
(38)
Распределение случайной величины tδ(n) получил английский химик и математик В.С. Госсет, публиковавший свои работы под псевдонимом "Стьюдент" (студент). Плотность вероятности распределения Стьюдента имеет вид:
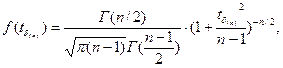 (39)
(39)
где Г (n) - гамма функция Эйлера, являющаяся обобщением понятия факториала.
На рис.5 приведены графика распределения Стьюдента для разных значений п. При 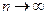 распределение (39) переходит в распределение Гаусса (23) и единичной дисперсией.
распределение (39) переходит в распределение Гаусса (23) и единичной дисперсией.
Распределение Стьюдента. аналогично распределению Гаусса, позволяет производить оценку точности результата измерений согласно выражению
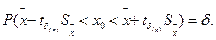 (40)
(40)
Только .теперь вместо 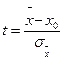 вводится коэффициент Стьюдента
вводится коэффициент Стьюдента 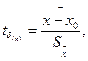 зависящий от числа измерений n и величины надежности δ .
зависящий от числа измерений n и величины надежности δ .

Рис. 5
Для коэффициентов Стьюдента составлены подробные таблицы. Ниже приводится небольшая часть из них.
Таблица 2
Дата добавления: 2015-08-01; просмотров: 742;
