Погрешности косвенных измерений
Часто приходится вычислять искомую величину по результатам измерений других величин, связанных с этой величиной определенной функциональной зависимостью. Например, объем шара 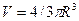 можно вычислить, измерив его радиус R . Также измерения называются косвенными.
можно вычислить, измерив его радиус R . Также измерения называются косвенными.
Рассмотрим конкретный пример. Допустим, что величины Х0, У0 и U0 связаны равенством
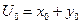 . (44)
. (44)
Непосредственно измеряются величины Х0 и У0, и по этим измерениям мы судим об U0, считая
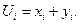 (45)
(45)
измерением величины U0.
Предполагается, что измерения Хi и yi независимы друг
от друга, и распределены нормально с дисперсиями 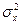 и
и 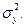 Задача заключается в том, как по известным значениям
Задача заключается в том, как по известным значениям 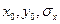 и
и 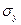 определить
определить 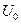 и
и 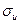 .
.
Очевидно, что погрешность косвенного измерения 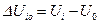 обусловлена погрешностями отдельных измерений
обусловлена погрешностями отдельных измерений 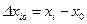 и
и 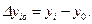 . Поэтому выражение (45) можно переписать в виде:
. Поэтому выражение (45) можно переписать в виде:
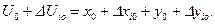 (46)
(46)
Вычитая почленно левые и правые части уравнений (46) и (44). для погрешности косвенного измерения получим:
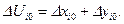 (47)
(47)
Тогда для дисперсии результатов косвенного измерения можно записать выражение:
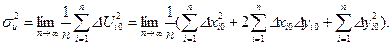
Здесь член 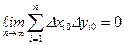 , так как любое произведение
, так как любое произведение 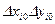 может быть с равной вероятностью или положительным, или отрицательным.
может быть с равной вероятностью или положительным, или отрицательным.
Учитывая, что 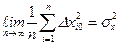 и
и 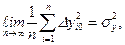
получим
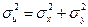 (48)
(48)
или 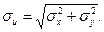 (49)
(49)
Равенство (49) определяет соотношение средних квадратичных ошибок прямых и косвенных измерений. Это выражение для частного случая имеет весьма общий характер и называется законом сложения дисперсий.
Следовательно, при измерении нескольких неизвестных величин складываются дисперсии этих величин (не ошибки, а именно дисперсии).
Средние квадратичные ошибки средних арифметических  связаны аналогичным образом
связаны аналогичным образом
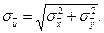 (50)
(50)
Рассмотрим общий случай, когда u - функция двух переменных х и y:
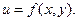 (51)
(51)
Ошибки в величинах х и у такова: 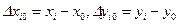 , где Х0 и У0 - истинные значения величин Х в У. Тогда для результата отдельного измерения можно записать
, где Х0 и У0 - истинные значения величин Х в У. Тогда для результата отдельного измерения можно записать
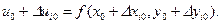 (52)
(52)
Если ‘та функция непрерывна и имеет производные, то ее можно разложить в ряд Тейлора. Рассматривая только члены c нулевыми и первыми степенями малых погрешностей 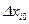 и
и 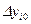 , получим:
, получим:
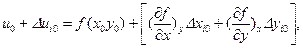
или поскольку 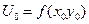
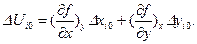 (53)
(53)
Частные производные здесь вычисляются при Х=Х0 и У=У0. Запишем выражение для дисперсии результатов косвенного измерения:
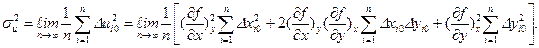
Учитывая, что
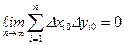 и
и 
получим
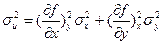 (54)
(54)
или
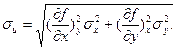 (55)
(55)
Для относительной погрешности косвенного измерения
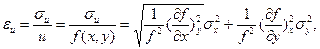
учитывая, что 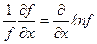 и
и 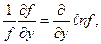 получим:
получим:
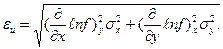 (56)
(56)
Дата добавления: 2015-08-01; просмотров: 749;
