Абсолютная и относительная погрешности. Формы записи данных

Определение 1.1.Если a - точное значение некоторой величины и a^* - известное приближение к нему, то абсолютной погрешностью приближенного значения a^* называют некоторую величину 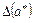, про которую известно, что

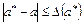. (1.1)

Определение 1.2.Относительной погрешностью приближенного значения называют некоторую величину 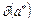, про которую известно, что

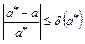. (1.2)

Относительную погрешность часто выражают в процентах.

Определение 1.3.Значащими цифрами числа называют все цифры в его записи, начиная с первой ненулевой слева.

Пример 1.1

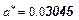
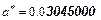
(Здесь цифры, записанные курсивом, значащие)

Определение 1.4.Значащую цифру называют верной, если модуль погрешности числа не превосходит единицы разряда, соответствующего этой цифре.

Пример 1.2

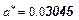
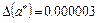
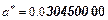
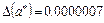
(Здесь цифры, записанные курсивом, верные)

Определение 1.5.Если все значащие цифры верные, то говорят, что число записано со всеми верными цифрами.

Иногда употребляется термин число верных цифр после запятой: подсчитывается число верных цифр после запятой от первой цифры до последней верной цифры.

Довольно часто информация о некоторой величине задается пределами измерений

.

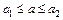Принято записывать эти пределы с одинаковым числом знаков после запятой, так как обычно достаточно грубого представления о погрешности. В записи чисел a₁, a₂ обычно берут столько значащих цифр, сколько нужно для того, чтобы разность 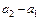содержала одну, две значащие цифры.

Информацию о том, что 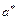является приближенным значением числа a с абсолютной погрешностью 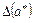, принято также записывать в виде

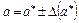. (1.3)

Числа 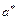, 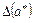принято записывать с одинаковым количеством знаков после запятой.

Пример 1.3

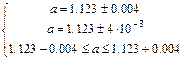
Информацию о том, что 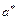является приближенным значением числа а с относительной погрешностью 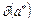записывают в виде

.

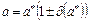Пример 1.4

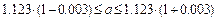
(Данная запись числа эквивалентна записи чисел из примера 1.2)