Метод простой итерации
Заменим уравнение (2.1) равносильным уравнением
x = f(x). (2.4)
Пусть x - корень уравнения (2.4), а x0, полученное каким либо способом нулевое приближение к корню x. Подставляя x0 в правую часть уравнения (2.4), получим некоторое число x1 = f(x0). Повторим данную процедуру с x1 и получим x2 = f(x1). Повторяя описанную процедуру, получим последовательность
x0, x1,…xn, …, (2.5)
называемую итерационной последовательностью.
Геометрическая интерпретация данного алгоритма представлена на рис. 2.6.
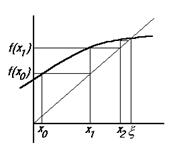
Рис. 2.6
Итерационная последовательность, вообще говоря, может быть как сходящейся, так и расходящейся, что определяется видом функции f(x).
Теорема 2.1. Если функция f(x) непрерывна, а последовательность (2.5) сходится, то предел последовательности (2.5) является корнем уравнения (2.4).
Действительно, пусть 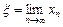 . Перейдем к пределу в равенстве
. Перейдем к пределу в равенстве 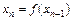 :
:
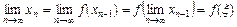 .(2.6)
.(2.6)
Условие сходимости итерационного процесса определяется теоремой о достаточном условии сходимости итерационного процесса.
Теорема 2.2. Пусть уравнение 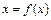 имеет единственный корень на отрезке
имеет единственный корень на отрезке 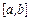 и выполнены условия:
и выполнены условия:
1)  определена и дифференцируема на
определена и дифференцируема на 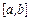 ;
;
2) 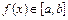 для всех
для всех  ;
;
3) существует такое вещественное q, что 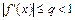 для всех
для всех  .
.
Тогда итерационная последовательность 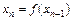 (n = 1, 2, …) сходится при любом начальном приближении
(n = 1, 2, …) сходится при любом начальном приближении 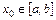 .
.
Доказательство. Построим итерационную последовательность вида (2.5) с любым начальным значением 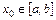 . В силу условия 2 теоремы 2.2 все члены последовательности находятся в отрезке
. В силу условия 2 теоремы 2.2 все члены последовательности находятся в отрезке 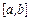 .
.
Рассмотрим два последовательных приближения 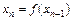 и
и 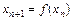 . По теореме Лагранжа о конечных приращениях имеем
. По теореме Лагранжа о конечных приращениях имеем
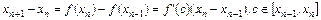 .
.
Переходя к модулям и принимая во внимание условие 3 теоремы 2.2, получим
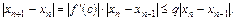
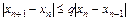 .
.
При n = 1, 2, … имеем
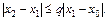
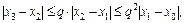 (2.7)
(2.7)
….
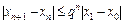 .
.
Рассмотрим ряд
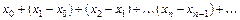 (2.8)
(2.8)
Составим частичные суммы этого ряда
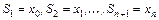 .
.
Заметим, что (n+1)-я частичная сумма ряда (2.8) совпадает с n-ым членом итерационной последовательности (2.5), т.е.
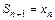 . (2.9)
. (2.9)
Сравним ряд (2.8) с рядом
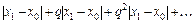 (2.10)
(2.10)
Заметим, что в силу соотношения (2.7) абсолютные величины членов ряда (2.8) не превосходят соответствующих членов ряда (2.10). Но ряд (2.10) сходится как бесконечно убывающая геометрическая прогрессия (q < 1, по условию). Следовательно, и ряд (2.8) сходится, т.е. его частичная сумма (2.9) имеет предел. Пусть 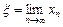 . В силу непрерывности функции f получаем (cм. (2.6)):
. В силу непрерывности функции f получаем (cм. (2.6)):
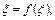
т.е. x - корень уравнения 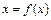 .
.
Отметим, что условия теоремы не являются необходимыми. Это означает, что итерационная последовательность может оказаться сходящейся и при невыполнении этих условий.
Найдем погрешность корня уравнения, найденного методом простой итерации. Пусть xn - приближение к истинному значению корня уравнения x = f(x). Абсолютная ошибка приближения xn оценивается модулем
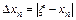 .
.
Принимая во внимание (2.8) и (2.9), имеем
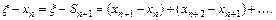 (2.11)
(2.11)
Сравним (2.11) с остатком ряда (2.9):
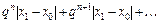 (2.12)
(2.12)
Учитывая оценку (2.7), получаем
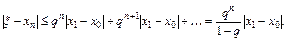
Таким образом, для оценки погрешности n-го приближения получается формула
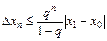 . (2.13)
. (2.13)
На практике удобнее использовать модификацию формулы (2.13).
Примем за нулевое приближение 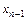 (вместо
(вместо 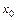 ). Следующим приближением будет
). Следующим приближением будет 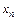 (вместо
(вместо  ).
).
Так как 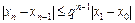 , то
, то
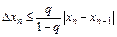 . (2.14)
. (2.14)
При заданной точности ответа e итерационный процесс прекращается, если 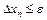 .
.
Дата добавления: 2015-08-21; просмотров: 1669;
