Метод половинного деления

Пусть уравнение (2.1) имеет на отрезке [a,b] единственный корень, причем функция F(x) на данном отрезке непрерывна (рис. 2.1).

Разделим отрезок [a,b] пополам точкой с=(a+b)/2. Если F(c)¹0, то возможны два случая:

1) функция F(x) меняет знак на отрезке [a,c];

2) функция F(x) меняет знак на отрезке [c,b].

Выбирая в каждом случае тот отрезок, на котором функция меняет знак, и продолжая процесс половинного деления дальше, можно дойти до сколь угодно малого отрезка, содержащего корень уравнения.

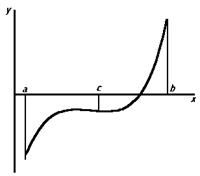
Рис. 2.1

Пример 2.1. Решение в пакете MATLAB методом половинного деления уравнения

1. Создание файла Func.m, содержащего описание функции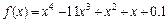

% листинг файла Func.m

function z=Func(x)

z=x.^4-11*x.^3+x.^2+x+0.1;

2. Создание файла Div2.m, содержащего описание функции, возвращающей значение корня уравнения 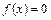методом половинного деления

% листинг файла Div2.m

function z=Div2(f,x1,x2,eps);

% имя m-файла, содержащего описание функции

% x1 - левая граница отрезка, на котором ищется решение

% уравнения

% x2 - правая граница отрезка, на котором ищется решение

% уравнения

% eps - точность решения

L=x2-x1;

while L>eps

c=(x2+x1)/2;

if feval(f,c)*feval(f,x1)<0

% feval(f,c) - оператор вычисления в точке x=c значения функции,

% описание, которой находится в соответствующем файле.

% Имя файла хранится в строковой переменной f

x2=c;

Else

x1=c;

End;

L=x2-x1;

End;

z=c;

3. Построение графика функции на интервале [-1,1]

>> x1=-1;

>> x2=1;

>> dx=10^-3;

>> x=x1:dx:x2;

>> plot(x,Func(x)); grid on

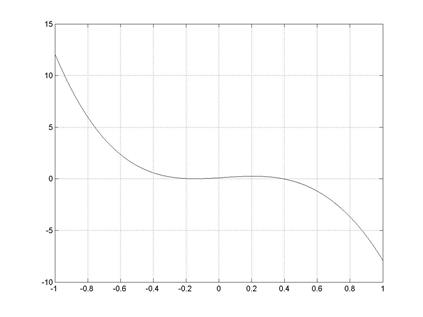
Рис. 2.2

4. Вычисление значения корня уравнения

>> Div2('Func',x1,x2,10^-5)

ans =

0.3942

5. Проверка полученного значения корня

>> Func(ans)

ans =

E-006

Для рассмотрения процесса нахождения корня уравнения в динамике, необходимо сохранить значение корня на каждом шаге вычислительной процедуры и построить зависимость значения корня от номера шага. Ниже приведен листинг файла Div2I.m, содержащего описание функции, возвращающей значение корня и длины отрезка, на котором данный корень находится, на каждом шаге метода половинного деления.

% листинг файла Div2I.m

function [z1,z2]=Div2(f,x1,x2,eps);

k=1;

L(1)=x2-x1;% начальная длина отрезка

c(1)=(x2+x1)/2;% начальное значение корня

while L(k)>eps

if feval(f,c(k))*feval(f,x1)<0

x2=c(k);

Else

x1=c(k);

End;

k=k+1;

c(k)=(x2+x1)/2;

L(k)=x2-x1;

End;

z1=c;

z2=L;

6. Вычисление значений корня и длины отрезка, на котором ищется решение, на каждом шаге итерационного процесса

>> [c L]=Div2I('Func',x1,x2,10^-5);

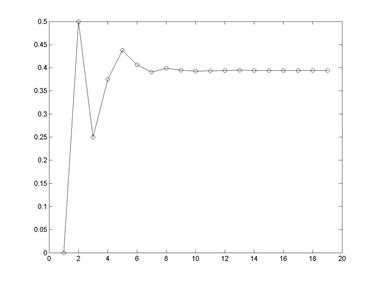
Рис. 2.3. Зависимость значения корня от номера шага вычислительной процедуры

5. Визуализации зависимости значения корня от номера итерационного процесса (рис. 2.3)

>> plot(c, '-o')

6. Визуализация зависимости длины отрезка, на котором ищется значение корня, от номера итерации (рис. 2.4)

>> plot(L, '-o')

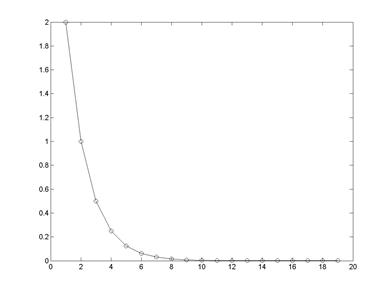
Рис. 2.4. Зависимость длины отрезка, на котором ищется значение корня, от номера шага вычислительной процедуры