Общие сведения и определения

Наиболее общий вид нелинейного уравнения:

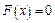, (2.1)

где функция 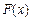определена и непрерывна на конечном или бесконечном интервале [a,b].

Определение 2.1. Всякое число xÎ[a,b], обращающее функцию F(x) в нуль, называется корнем уравнения (2.1).

Определение 2.2.Число x называется корнем k-ой кратности, если при x=x вместе с функцией F(x) равны нулю ее производные до (k-1)-гопорядка включительно:

F(x)=F¢(x)=…=F^(k-1)(x)=0. (2.2)

Определение 2.3.Однократный корень называется простым.

Определение 2.4.Уравнения F(x)=0и G(x)=0называются равносильными (эквивалентными), если множества решений данных уравнений совпадают.

Нелинейные уравнения с одной переменной подразделяются на алгебраическиеи трансцендентные.

Определение 2.5.Уравнение (2.1) называется алгебраическим, если функция является алгебраической.

Путем алгебраических преобразований из всякого алгебраического уравнения можно получить уравнение в канонической форме:

P_n(x)=a₀xⁿ+a₁x^n-1+…+a_n, (2.3)

где a₀, a₁,…, a_n - коэффициенты уравнения, x - неизвестное.

Из алгебры известно, что всякое алгебраическое уравнение имеет, по крайней мере, один вещественный или один комплексный корень.

Определение 2.6.Уравнение (2.1) называется трансцендентным, если функция F(x) не является алгебраической.

Определение 2.7. Решить уравнение (2.1) означает:

1) установить имеет ли уравнение корни;

2) определить число корней уравнения;

3) найти значения корней уравнения с заданной точностью.