Занятие №57. Регрессионный анализ. Проверка значимости и интервальное оценивание коэффициентов регрессии

№1. Имеются данные (условные) о сменной добыче угля на одного рабочего 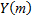и мощности пласта 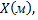характеризующие процесс добычи угля в 10 шахтах.

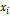
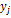
Оценить сменную среднюю добычу угля на одного рабочего для шахт с мощностью пласта 8 метров. Найти 95% доверительные интервалы для индивидуального и среднего значений сменной добычи угля на 1 рабочего для таких же шахт.

Примечание: вначале составим уравнение регрессии

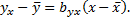
Вычислим все необходимые суммы по формулам:

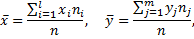
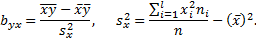
Получим

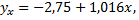
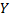т.е. при увеличении мощности пласта на 1 м добыча угля на одного рабочего увеличивается в среднем на 1,016 т (в условных единицах). Надо оценить условное математическое ожидание 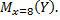Выборочной оценкой 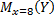является групповая средняя 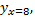которую найдем по уравнению регрессии

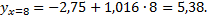
Для построения доверительного интервала для 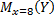необходимо знать дисперсию его оценки, т.е. 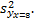Составим вспомогательную таблицу с учетом того, что 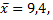а значения 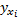определяется по полученному уравнению регрессии.

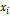
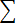
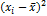
	1,96	2,56	6,76	0,16	1,96	1,96	0,16	0,16	1,96	6,76	24,40
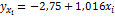
	5,38	8,43	9,44	6,39	5,38	5,38	6,39	6,39	5,38	9,44	-
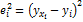
	0,14	2,48	0,31	0,37	0,14	0,39	0,15	1,94	0,39	2,08	8,39

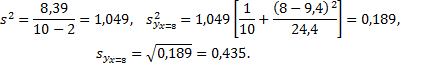
По таблице приложений находим 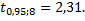Искомый доверительный интервал

Средняя сменная добыча угля на одного рабочего для шахт с мощностью пласта 8 м с надежностью 0,95 находится в пределах от 4,38 до 6,38 т.

Чтобы построить доверительный интервал для индивидуального значения 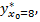найдем дисперсию его оценки

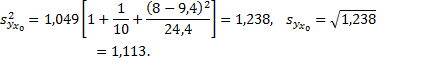
Искомый доверительный интервал

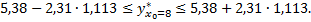
Таким образом, индивидуальная сменная добыча угля на одного рабочего для шахт с мощностью пласта 8 м с надежностью 0,95 находится в пределах от 2,81 до 7,95.

№2. По данным таблицы исследовать зависимость урожайности зерновых культур 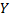(ц/га) от количества осадков (см), выпавших в вегетационный период.

№

Количество осадков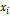

Урожайность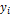

Примечание: из качественных соображений можно предположить, что увеличение количества выпавших осадков приводит к увеличению урожайности до некоторого предела, после чего урожайность будет снижаться. Если построить точки корреляционного поля, можно предположить, что наиболее подходящим уравнением регрессии будет уравнение параболы

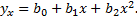
Параметры находим, применяя метод наименьших квадратов

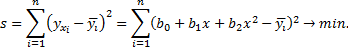
Приравнивая частные производные

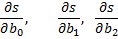
нулю, получим после преобразований систему нормальных уравнений

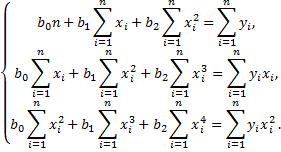
Для расчета необходимых сумм составим вспомогательную таблицу

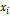
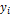
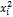
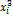
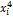
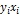
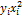
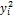
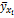
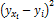
									21,7	1,69
									24,3	0,11
…	…	…	…	…	…	…	…	…	…	…
									24,7	0,46
									23,4	2,44
									-	45,94

Теперь система примет вид

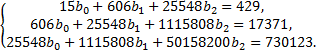
Решая эту систему методом Гаусса, получим 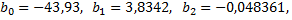т.е. уравнение регрессии имеет вид

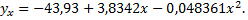
Оценим значимость полученной зависимости. С этой целью найдем суммы

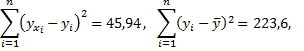
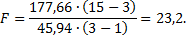
Табличное значение 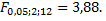Так как 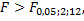то уравнение регрессии значимо.

Для оценки тесноты связи вычислим индекс корреляции

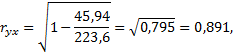
т.е. полученная зависимость весьма тесная. Коэффициент детерминации 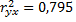показывает, что вариация урожайности зерновых культур на 79,5% обусловлена регрессией, или изменчивостью количества выпавших в вегетационный период осадков.