Критические точки распределения F Фишера-Снедекора
( 
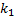– число степеней свободы большей дисперсии,
– число степеней свободы меньшей дисперсии)
Уровень значимости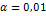 
| ||||||||||||
| 
| |||||||||||
| 98,49 | 99,01 | 99,17 | 99,25 | 99,30 | 99,33 | 99,34 | 99,36 | 99,38 | 99,40 | 99,41 | 99,42 | |
| 34,12 | 30,81 | 29,46 | 28,71 | 28,24 | 27,91 | 27,67 | 27,49 | 27,34 | 27,23 | 27,13 | 27,05 | |
| 21,20 | 18,00 | 16,69 | 15,98 | 15,52 | 15,21 | 14,98 | 14,80 | 14,66 | 14,54 | 14,45 | 14,37 | |
| 16,26 | 13,27 | 12,06 | 11,39 | 10,97 | 10,67 | 10,45 | 10,27 | 10,15 | 10,05 | 9,96 | 9,89 | |
| 13,74 | 10,92 | 9,78 | 9,15 | 8,75 | 8,47 | 8,26 | 8,10 | 7,98 | 7,87 | 7,79 | 7,72 | |
| 12,25 | 9,55 | 8,45 | 7,85 | 7,46 | 7,19 | 7,00 | 6,84 | 6,71 | 6,62 | 6,54 | 6,47 | |
| 11,26 | 8,65 | 7,59 | 7,01 | 6,63 | 6,37 | 6,19 | 6,03 | 5,91 | 5,82 | 5,74 | 5,67 | |
| 10,56 | 8,02 | 6,99 | 6,42 | 6,06 | 5,80 | 5,62 | 5,47 | 5,35 | 5,26 | 5,18 | 5,11 | |
| 10,04 | 7,56 | 6,55 | 5,99 | 5,64 | 5,39 | 5,21 | 5,06 | 4,95 | 4,85 | 4,78 | 4,71 | |
| 9,86 | 7,20 | 6,22 | 5,67 | 5,32 | 5,07 | 4,88 | 4,74 | 4,63 | 4,54 | 4,46 | 4,40 | |
| 9,33 | 6,93 | 5,95 | 5,41 | 5,06 | 4,82 | 4,65 | 4,50 | 4,39 | 4,30 | 4,22 | 4,16 | |
| 9,07 | 6,70 | 5,74 | 5,20 | 4,86 | 4,62 | 4,44 | 4,30 | 4,19 | 4,10 | 4,02 | 3,96 | |
| 8,86 | 6,51 | 5,56 | 5,03 | 4,69 | 4,46 | 4,28 | 4,14 | 4,03 | 3,94 | 3,86 | 3,80 | |
| 8,68 | 6,36 | 5,42 | 4,89 | 4,56 | 4,32 | 4,14 | 4,00 | 3,89 | 3,80 | 3,73 | 3,67 | |
| 8,53 | 6,23 | 5,29 | 4,77 | 4,44 | 4,20 | 4,03 | 3,89 | 3,78 | 3,69 | 3,61 | 3,55 | |
| 8,40 | 6,11 | 5,18 | 4,67 | 4,34 | 4,10 | 3,93 | 3,79 | 3,68 | 3,59 | 3,52 | 3,45 | |
Уровень значимости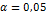 
| ||||||||||||
| 18,51 | 19,00 | 19,16 | 19,25 | 19,30 | 19,33 | 19,36 | 19,37 | 19,38 | 19,39 | 19,40 | 19,41 | |
| 10,13 | 9,55 | 9,28 | 9,12 | 9,01 | 8,94 | 8,88 | 8,84 | 8,81 | 8,78 | 8,76 | 8,74 | |
| 7,71 | 6,94 | 6,59 | 6,39 | 6,26 | 6,16 | 6,09 | 6,04 | 6,00 | 5,96 | 5,93 | 5,91 | |
| 6,61 | 5,79 | 5,41 | 5,19 | 5,05 | 4,95 | 4,88 | 4,82 | 4,78 | 4,74 | 4,70 | 4,68 | |
| 5,99 | 5,14 | 4,76 | 4,53 | 4,39 | 4,28 | 4,21 | 4,15 | 4,10 | 4,06 | 4,03 | 4,00 | |
| 5,59 | 4,74 | 4,35 | 4,12 | 3,97 | 3,87 | 3,79 | 3,73 | 3,68 | 3,63 | 3,60 | 3,57 | |
| 5,32 | 4,46 | 4,07 | 3,84 | 3,69 | 3,58 | 3,50 | 3,44 | 3,39 | 3,34 | 3,31 | 3,28 | |
| 5,12 | 4,26 | 3,86 | 3,63 | 3,48 | 3,37 | 3,29 | 3,23 | 3,18 | 3,13 | 3,10 | 3,07 | |
| 4,96 | 4,10 | 3,71 | 3,48 | 3,33 | 3,22 | 3,14 | 3,07 | 3,02 | 2,97 | 2,94 | 2,91 | |
| 4,84 | 3,98 | 3,59 | 3,36 | 3,20 | 3,09 | 3,01 | 2,95 | 2,90 | 2,86 | 2,82 | 2,79 | |
| 4,75 | 3,88 | 3,49 | 3,26 | 3,11 | 3,00 | 2,92 | 2,85 | 2,80 | 2,76 | 2,72 | 2,69 | |
| 4,67 | 3,80 | 3,41 | 3,18 | 3,02 | 2,92 | 2,84 | 2,77 | 2,72 | 2,67 | 2,63 | 2,60 | |
| 4,60 | 3,74 | 3,34 | 3,11 | 2,96 | 2,85 | 2,77 | 2,70 | 2,65 | 2,60 | 2,56 | 2,53 | |
| 4,54 | 3,68 | 3,29 | 3,06 | 2,90 | 2,79 | 2,70 | 2,64 | 2,59 | 2,55 | 2,51 | 2,48 | |
| 4,49 | 3,63 | 3,24 | 3,01 | 2,85 | 2,74 | 2,66 | 2,59 | 2,54 | 2,49 | 2,45 | 2,42 | |
| 4,45 | 3,59 | 3,20 | 2,96 | 2,81 | 2,70 | 2,62 | 2,55 | 2,50 | 2,45 | 2,41 | 2,38 |
Приложение 8
Критические точки критерия Вилкоксона
| Объемы выборок |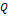 
| Объемы выборок |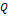
| |||||||||
| 
| 0,005 | 0,01 | 0,025 | 0,05 |
|
| 0,005 | 0,01 | 0,025 | 0,05 | |
| Объемы выборок |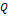
| Объемы выборок |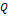
| |||||||||
|
|
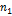
| 0,005 | 0,01 | 0,025 | 0,05 |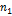
|
| 0,005 | 0,01 | 0,025 | 0,05 | |
ОГЛАВЛЕНИЕ
| Введение ………………………………………………………… | |
| Лекция №1. Матрицы. Определители и их свойства ………… | |
| Лекция №2. Формулы Крамера. Матричный способ решения систем линейных алгебраических уравнений ………………… | |
| Лекция №3. Метод Гаусса решения систем линейных алгебраических уравнений. Однородные системы линейных алгебраических уравнений ……………………………………. | |
| Лекция №4. Векторы …………………………………………… | |
| Лекция №5. Евклидово пространство. Линейные пространства | |
| Лекция №6. Линейные преобразования ………………………… | |
| Лекция №7. Уравнение линии на плоскости …………………… | |
| Лекция №8. Линии второго порядка …………………………… | |
| Лекция №9. Плоскость ………………………………………… | |
| Лекция №10. Прямая в пространстве и ее уравнения ………… | |
| Лекция №11. Поверхности второго порядка …………………… | |
| Лекция №12. Функция. Основные элементарные функции. Предел функции ………………………………………………… | |
| Лекция №13. Непрерывность функции в точке и на интервале | |
| Лекция №14. Производная функции …………………………… | |
| Лекция №15. Основные теоремы о дифференцируемых функциях ………………………………………………………… | |
| Лекция №16. Применение производной к исследованию функций …………………………………………………………… | |
| Лекция №17. Функции многих переменных ………………… | |
| Лекция №18. Экстремум функции двух переменных ………… | |
| Лекция №19. Неопределенный интеграл ……………………… | |
| Лекция №20. Интегрирование по частям ……………………… | |
| Лекция №21. Методы интегрирования ………………………… | |
| Лекция №22. Интегрирование тригонометрических функций | |
| Лекция №23. Интегрирование иррациональных функций …… | |
| Лекция №24. Определенный интеграл ……………………… | |
| Лекция №25. Приложения определенного интеграла ………… | |
| Лекция №26. Несобственные интегралы …………………… | |
| Лекция №27. Двойной интеграл ……………………………… | |
| Лекция №28. Приложения двойного интеграла ………………… | |
| Лекция №29. Криволинейный интеграл ……………………… | |
| Лекция №30. Комплексные числа …………………………… | |
| Лекция №31. Дифференциальные уравнения ………………… | |
| Лекция №32.Линейные дифференциальные уравнения первого порядка. Уравнения Бернулли …………………………………… | |
| Лекция №33. Дифференциальные уравнения высших порядков | |
| Лекция №34. Линейные неоднородные дифференциальные уравнения второго порядка …………………………………… | |
| Лекция №35. Системы дифференциальных уравнений …… | |
| Лекция №36. Применение аппарата дифференциальных уравнений в механике ………………………………………… | |
| Лекция №37. Числовые ряды ………………………………… | |
| Лекция №38. Знакопеременные ряды …………………………… | |
| Лекция №39. Функциональные ряды …………………………… | |
| Лекция №40. Разложение функций в степенные ряды ………… | |
| Лекция №41. Ряды Фурье ……………………………………… | |
| Лекция № 42. Множества ………………………………………… | |
| Лекция №43. Основы теории графов. Элементы комбинаторики ………………………………………………….. | |
| Лекция №44. Вероятность события …………………………… | |
| Лекция №45. Повторные независимые испытания …………… | |
| Лекция №46. Случайные величины ………………………… | |
| Лекция №47. Законы распределения случайных величин …… | |
| Лекция №48. Закон больших чисел ………………………… | |
| Лекция №49. Выборочный метод …………………………… | |
| Лекция №50. Статистические оценки параметров распределения ………………………………………………….. | |
| Лекция №51. Статистическая проверка гипотез ……………… | |
| Лекция №52. Дисперсионный анализ …………………………… | |
| Лекция №53. Корреляционно – регрессионный анализ ……… | |
| Лекция №54. Понятие о многомерном корреляционном анализе …………………………………………………………. | |
| Занятие №1. Определители и их свойства …………………… | |
| Занятие № 2. Алгебра матриц ………………………………… | |
| Занятие №3. Формулы Крамера. Матричный способ решения систем линейных алгебраических уравнений. Решение систем линейных алгебраических уравнений методом Гаусса ……… | |
| Занятие №4. Критерий Кронекера – Капелли совместности систем линейных алгебраических уравнений. Общее, базисное, частные решения. Однородные системы линейных алгебраических уравнений ………………………………….. | |
| Занятие №5. Векторы. Основные понятия …………………… | |
| Занятие №6. Векторное, скалярное и смешанное произведение векторов …………………………………………………………. | |
| Занятие №7. Уравнение линии на плоскости ………………… | |
| Занятие №8. Линии второго порядка ………………………… | |
| Занятие №9. Приведение общего уравнения кривых второго порядка к каноническому виду ………………………………… | |
| Занятие №10. Плоскость ……………………………………… | |
| Занятие №11. Прямая в пространстве ………………………… | |
| Занятие №12. Каноническое уравнение поверхностей второго порядка ………………………………………………………….. | |
| Занятие №13. Функция. Вычисление пределов функции …… | |
| Занятие №14. «Замечательные» пределы. Непрерывность функции в точке и на интервале ………………………………… | |
| Занятие №15. Производная функции …………………………… | |
| Занятие №16. Дифференциал функции. Правило Лопиталя … | |
| Занятие №17. Применение производной к исследованию функций ………………………………………………………… | |
| Занятие №18. Функции многих переменных ………………… | |
| Занятие №19. Экстремум функции двух переменных ……… | |
| Занятие №20. Неопределенный интеграл ……………………… | |
| Занятие № 21. Интегрирование посредством замены переменной ……………………………………………………… | |
| Занятие №22. Интегрирование по частям. Интеграл от функций, содержащих квадратный двучлен ………………… | |
| Занятие № 23. Интегрирование рациональных функций ……… | |
| Занятие № 24. Интегрирование тригонометрических функций | |
| Занятие № 25. Интегрирование некоторых иррациональных функций ………………………………………………………….. | |
| Занятие №26. Определенный интеграл ……………………… | |
| Занятие №27. Механические приложения определенного интеграла ………………………………………………………… | |
| Занятие №28. Вычисление несобственных интегралов ……… | |
| Занятие №29. Вычисление двойного интеграла ……………… | |
| Занятие №30. Приложения двойного интеграла ……………… | |
| Занятие №31. Криволинейный интеграл ……………………… | |
| Занятие №32. Комплексные числа …………………………… | |
| Занятие №33. Дифференциальные уравнения с разделяющимися переменными ………………………………… | |
| Занятие №34. Дифференциальные уравнения первого порядка. Уравнения Бернулли …………………………………………… | |
| Занятие №35. Дифференциальные уравнения высших порядков, допускающие понижение степени ………………… | |
| Занятие №36. Интегрирование линейных однородных дифференциальных уравнений второго порядка с постоянными коэффициентами ………………………………………………… | |
| Занятие №37. Неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами …………… | |
| Занятие №38. Задачи, приводящие к дифференциальным уравнениям …………………………………………………….. | |
| Занятие №39. Числовые ряды с положительными членами …… | |
| Занятие №40. Знакопеременные числовые ряды …………… | |
| Занятие №41. Степенные ряды ………………………………… | |
| Занятие №42. Ряды Тейлора …………………………………… | |
| Занятие №43. Применение рядов к приближенным вычислениям …………………………………………………….. | |
| Занятие №44. Разложение функций в ряд Фурье ……………… | |
| Занятие №45. Операции над множествами. Основные тождества алгебры множеств ………………………………… | |
| Занятие №46. Комбинаторика. Определение вероятности события ……………………………………………………………. | |
| Занятие №47. Теоремы сложения и умножения вероятностей. Формула полной вероятности …………………………………… | |
| Занятие №48. Повторные независимые испытания …………… | |
| Занятие №49. Дискретные случайные величины. Закон распределения дискретной случайной величины …………… | |
| Занятие №50. Непрерывные случайные величины. Числовые характеристики непрерывных случайных величин. Законы распределения непрерывной случайной величины …………… | |
| Занятие №51. Законы распределения непрерывной случайной величины ……………………………………………………….. | |
| Занятие №52. Выборочный метод …………………………… | |
| Занятие №53. Статистические оценки параметров распределения …………………………………………………… | |
| Занятие №54. Эмпирические и выравнивающие частоты. Статистическая проверка гипотез ……………………………… | |
| Занятие №55. Корреляционный анализ ……………………… | |
| Занятие №56. Двухфакторный дисперсионный анализ ……… | |
| Занятие №57. Регрессионный анализ. Проверка значимости и интервальное оценивание коэффициентов регрессии ………… | |
| Словарь терминов и определений …………………………… | |
| Алфавитно-предметный указатель …………………………… | |
| Рекомендуемая литература …………………………………… | |
| Приложения ……………………………………………………… |
Учебное издание
Дата добавления: 2015-08-11; просмотров: 1195;